- dxd 的博客
[B1-2:算法之高精度算法]
- @ 2024-1-31 18:18:42
首先回顾各种整数数据类型的数值范围:
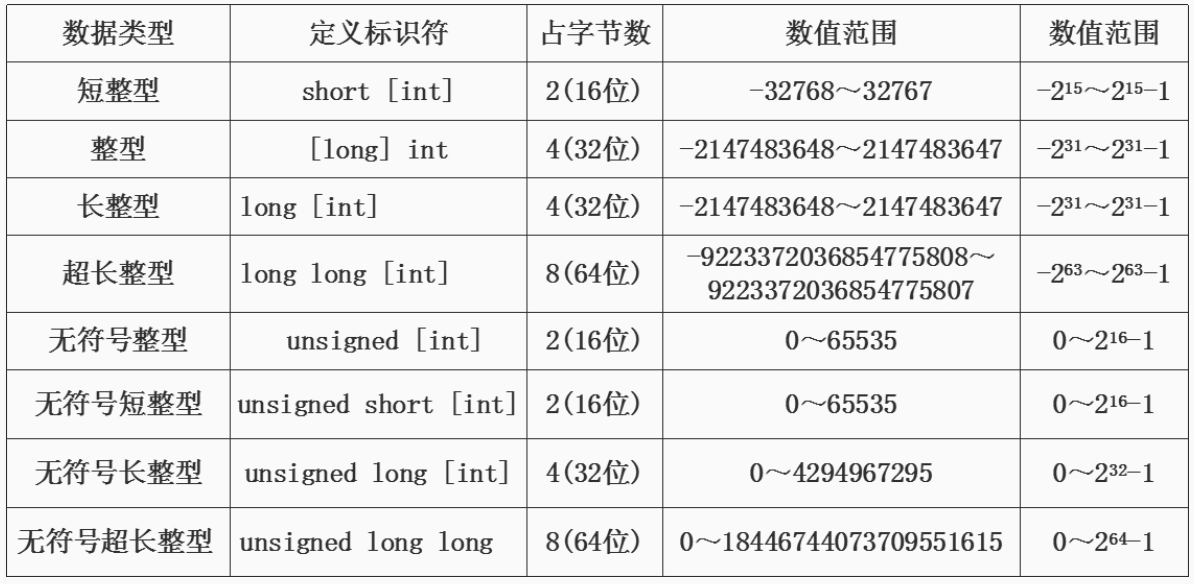
显然上述任何数据类型都无法满足下列式子的计算和存储,例如:
123456789012345678901234567890+1=123456789012345678901234567891
当运算超出上述范围时候,就需要用高精度算法来存储和计算了。
一、高精度加法
高精度加法运算就是模拟数学中的竖式计算的一个过程:
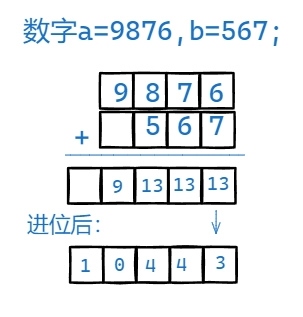
用字符串数组来模拟上述过程:
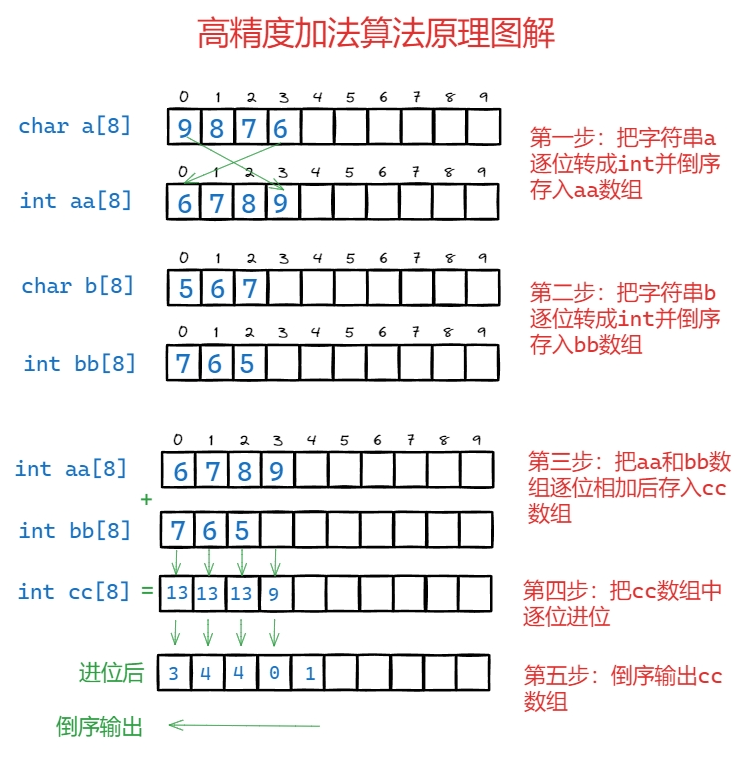
代码实现:
//高精度加法标准原理写法
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+5;//1005; 常量
int n;//变量
char a[N],b[N];
int aa[N],bb[N],cc[N],ka=0,kb=0;
int main() {
cin>>a>>b;
int lena=strlen(a),lenb=strlen(b);
int lenc=max(lena,lenb);
for(int i=0;i<lena;i++){//把a转为int并倒序存入aa
aa[lena-i-1] =a[i]-'0';
}
for(int i=lenb-1;i>=0;i--){//把b转为int并倒序存入bb(方法二)
bb[lenb-i-1]=b[i]-'0';
//bb[kb++]=b[i]-'0';//和上一行作用一样
}
for(int i=0;i<lenc;i++){//aa,bb对应位置相加存入cc
cc[i]=aa[i]+bb[i];
}
for(int i=0;i<lenc;i++){//逐位检查是否有进位
cc[i+1]+=cc[i]/10;//进位存入高位
cc[i]%=10;//cc[i]=cc[i]%10;
}
if(cc[lenc])lenc++;//特判一下最高位是否有数字
for(int i=lenc-1;i>=0;i--)cout<<cc[i];//倒序输出cc即为a+b的答案
return 0;
}
//高精度加法二
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+5;//1005; 常量
char a[N],b[N];
int cc[N];
int main() {
cin>>a>>b;
int ka=strlen(a)-1,kb=strlen(b)-1,kc=0;
while(ka>=0 && kb>=0){//a[ka]+a[kb]存入对应的cc[kc]
cc[kc++]+=a[ka--]-'0'+b[kb--]-'0';
cc[kc]+=cc[kc-1]/10;cc[kc-1]%=10;
}
while(ka>=0){//如果a比较长还没加完
cc[kc++]=a[ka--]-'0';//把a多余的部分搬到cc后面
cc[kc]+=cc[kc-1]/10;cc[kc-1]%=10;
}
while(kb>=0){//如果b比较长还没加完
cc[kc++]=b[kb--]-'0';//把n多余的部分搬到cc后面
cc[kc]+=cc[kc-1]/10;cc[kc-1]%=10;
}
if(!cc[kc])kc--;//判断高位是否有数
for(int i=kc;i>=0;i--)cout<<cc[i];
return 0;
}
精简版代码图解
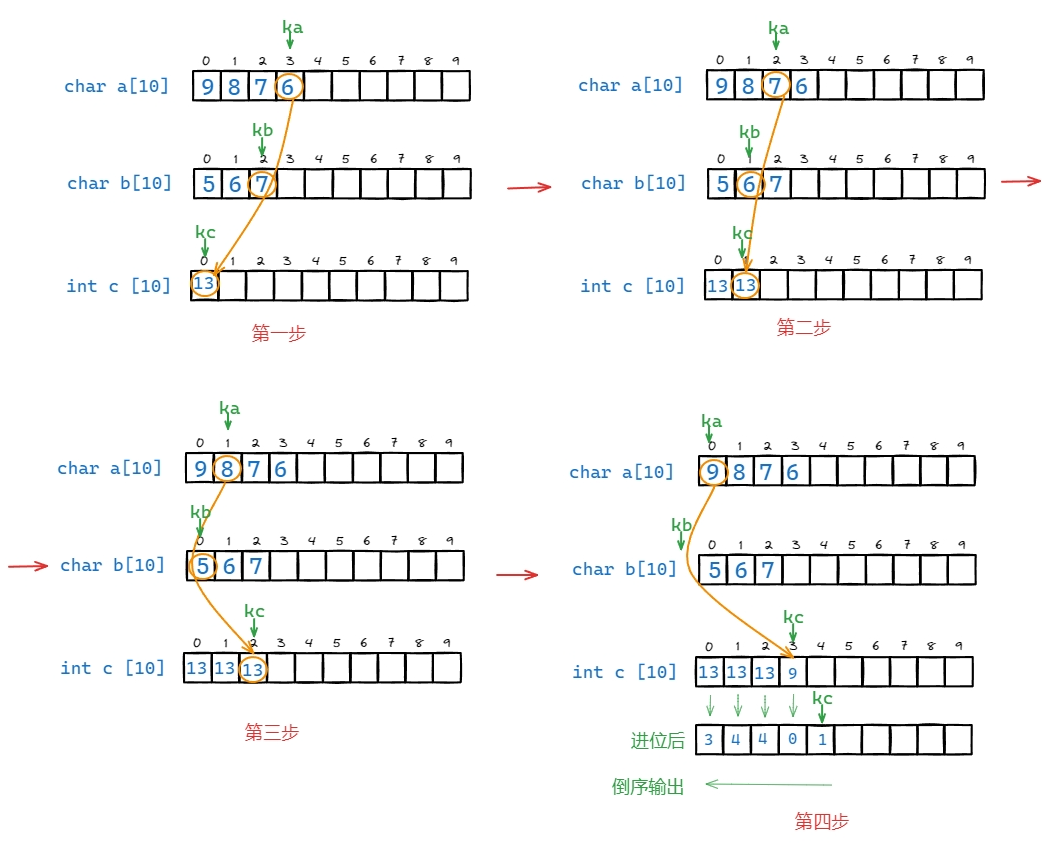
//高精度加法代码精简版
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+5;//1005; 常量
char a[N],b[N];
int c[N];
int main() {
cin>>a>>b;
int ka=strlen(a)-1,kb=strlen(b)-1,kc=0;
//三个模拟指针,ka,kb分别指向a,b数组最高位,kc指向c数组最低位
while(ka>=0 || kb>=0){//只要还没加完
if(ka>=0)c[kc]+=a[ka--]-'0';//a[ka]没有加完则加入c[kc]中
if(kb>=0)c[kc]+=b[kb--]-'0';//同理,a[kb]合法则加入c[kc]中
c[kc+1]+=c[kc]/10;c[kc]%=10;//同时检查c[kc]进位给高位
kc++; //kc后移一位
}
if(!c[kc])kc--;//判断高位是否有数
for(int i=kc;i>=0;i--)cout<<c[i];
return 0;
}
高精度减法1
#include <bits/stdc++.h>
using namespace std;
string aa,bb;
bool flag=0;//默认符号为正数
int a[1005],b[1005],c[1005];
void look(int x[],int k){
cout<<endl;
for(int i=0;i<=k;i++){
cout<<x[i]<<" ";
}
cout<<endl;
}
int main() {
cin>>aa>>bb;
int la=aa.size(),lb=bb.size();
//确保a>b;
if(la<lb || (la==lb&&aa<bb)){
flag=1;//flag为1说明结果为负数
swap(aa,bb);
swap(la,lb);
}
for(int i=0;i<la;i++)//aa转为int倒序存储
a[i]=aa[la-i-1]-'0';
for(int i=0;i<lb;i++)//bb转为int倒序存储
b[i]=bb[lb-i-1]-'0';
for(int i=0;i<la;i++){//逐位相减
c[i]=a[i]-b[i];
}
for(int i=0;i<la;i++){//检查借位
if(c[i]<0){
c[i+1]--;
c[i]+=10;
}
}
int lc=la;
while(lc>0 && !c[lc])lc--;//删除前导0
if(flag)cout<<"-";
for(int i=lc;i>=0;i--) cout<<c[i];
return 0;
}
//高精度减法 2
#include <bits/stdc++.h>
using namespace std;
string aa,bb;
bool flag=0;//默认符号为正数
int a[1005],b[1005],c[1005];
int main() {
cin>>aa>>bb;
int la=aa.size(),lb=bb.size();
//确保a>b;
if(la<lb || (la==lb&&aa<bb)){
flag=1;//flag为1说明结果为负数
swap(aa,bb);swap(la,lb);
}
for(int i=0;i<lb;i++)//bb转为int倒序存储
b[i]=bb[lb-i-1]-'0';
for(int i=0;i<la;i++){
a[i]=aa[la-i-1]-'0';//aa转为int倒序存储
c[i]=a[i]-b[i];//逐位相减
if(c[i]<0){//检查借位
c[i+1]--;
c[i]+=10;
}
}
int lc=la;
while(lc>0 && !c[lc])lc--;//删除前导0
if(flag)cout<<"-";
for(int i=lc;i>=0;i--) cout<<c[i];
return 0;
}
//高精度减法 3
#include <bits/stdc++.h>
using namespace std;
string a,b;
bool flag=0;//默认符号为正数
int c[1005];
int main() {
cin>>a>>b;
int la=a.size(),lb=b.size();
//确保a>b;
if(la<lb || (la==lb&&a<b)){
flag=1;//flag为1说明结果为负数
swap(a,b);swap(la,lb);
}
int pa=la-1,pb=lb-1,pc=0;
while(pa>=0){
c[pc++]=a[pa--]-'0'-(b[pb--]-48);//逐位相减
if(c[pc-1]<0){//检查借位
c[pc]--;
c[pc-1]+=10;
}
}
while(pc>0 && !c[pc])pc--;//删除前导0
if(flag)cout<<"-";
for(int i=pc;i>=0;i--) cout<<c[i];
return 0;
}
//高精度乘法带符号
#include <bits/stdc++.h>
using namespace std;
string aa,bb;
int flaga=1,flagb=1;//默认符号为正数
int a[1005],b[1005],c[1005];
int main() {
cin>>aa>>bb;
//特判符号部分
if(aa[0]=='-'){
flaga=-1;//符号标记
aa.erase(0,1);//删除符号
};
if(bb[0]=='-'){
flagb=-1;//符号标记
bb.erase(0,1);//删除符号
};
//特判符号部分
int la=aa.size(),lb=bb.size(),lc=la+lb;
for(int i=0;i<la;i++)//aa转为int倒序存储
a[i]=aa[la-i-1]-'0';
for(int i=0;i<lb;i++)//bb转为int倒序存储
b[i]=bb[lb-i-1]-'0';
for(int i=0;i<la;i++){
for(int j=0;j<lb;j++){//逐位相乘
c[i+j]+=a[i]*b[j];
}
}
for(int i=0;i<lc;i++){//处理进位
c[i+1]+=c[i]/10;
c[i]%=10;;
}
while(lc>0 && !c[lc])lc--;//删除前导0
if(flaga*flagb<0)cout<<'-';//输出符号
for(int i=lc;i>=0;i--) cout<<c[i];
return 0;
}
//高精度乘法带符号2
#include <bits/stdc++.h>
using namespace std;
string aa,bb;
int flaga=1,flagb=1,begina,beginb;//默认符号为正数
int a[1005],b[1005],c[1005];
void look(int x[],int k){
cout<<endl;
for(int i=0;i<=k;i++){
cout<<x[i]<<" ";
}
cout<<endl;
}
int main() {
cin>>aa>>bb;
int la=aa.size(),lb=bb.size(),lc=la+lb;
if(aa[0]=='-')flaga=-1,begina=1;//符号为处理
if(bb[0]=='-')flagb=-1,beginb=1;//符号为处理
for(int i=begina;i<la;i++)//aa转为int倒序存储
a[i-begina]=aa[la-i-1+begina]-'0';
for(int i=beginb;i<lb;i++)//bb转为int倒序存储
b[i-beginb]=bb[lb-i-1+beginb]-'0';
for(int i=0;i<la;i++){
for(int j=0;j<lb;j++){//逐位相乘
c[i+j]+=a[i]*b[j];
}
}
for(int i=0;i<lc;i++){//处理进位
c[i+1]+=c[i]/10;
c[i]%=10;;
}
while(lc>0 && !c[lc])lc--;//删除前导0
if(flaga*flagb<0)cout<<'-';
for(int i=lc;i>=0;i--) cout<<c[i];
return 0;
}
//高精度除以单精度
#include <bits/stdc++.h>
using namespace std;
string aa;
bool flag=0;//默认符号为正数
long long a[1005],b,c[1005],r,pc=0;
int main() {
cin>>aa>>b;
int la=aa.size(),lc=la;
for(int i=0;i<la;i++)//aa转为int倒序存储
a[i]=aa[i]-'0';
for(int i=0;i<la;i++){
c[i]=(r*10+a[i])/b;
r=(r*10+a[i])%b;
}
while(pc<la && !c[pc])pc++;//删除前导0
for(int i=pc;i<lc;i++) cout<<c[i];
//cout<<endl<<r;//输出余数
return 0;
}
