- gf24118 的博客
GF2025C2容斥原理&错位排列
- @ 2025-8-11 10:54:30
容斥原理&错位排列!!!
前言
容斥原理
容斥原理基础
为了深入理解,咱先举个栗子。
现有15人爱吃土豆,8人爱吃马铃薯,而爱吃土豆和马铃薯的共有4人,问只爱吃一种的人共有多少人。
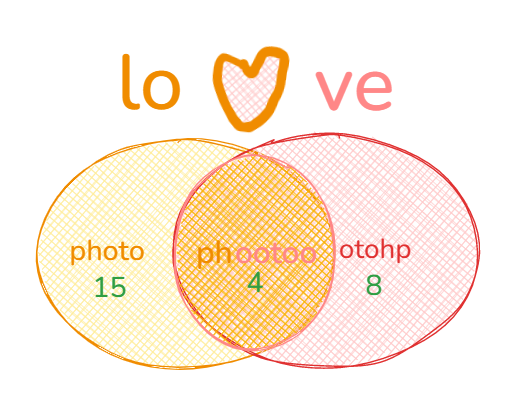
只要你今天带了脑子看此博客, 你就会惊奇的发现:这个问题的答案不就是吗?(当然不是,真要较真扣题目字眼我也没办法doge)
好吧言归正传,答案便是人。
如果我再加一个番茄呢?
为了叙述方便,我们把喜欢土豆、马铃薯、番茄的集合分别用 表示,则总数等于 。刚才已经讲过,如果把这三个集合的元素个数 直接加起来,会有一些元素重复统计了,因此需要扣掉 ,,,但这样一来,又有一小部分多扣了,需要加回来,即 。即
$$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|B\cap C|-|C\cap A|+|A\cap B\cap C|$$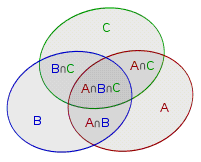
把上述问题推广到一般情况,就是我们熟知的容斥原理。
容斥原理的计算
全集 即为 的排列,;属性就是 . 套用补集的公式,问题变成求 .
可以知道,的含义是满足 的排列的数量。用容斥原理把问题式子展开,需要对若干个特定的集合的交集求大小,即:
其中省略了 的条件以方便表示。上述 个集合的交集表示有 个变量满足 的排列数,而剩下 个数的位置任意,因此排列数:
那么选择 个元素的方案数为 ,因此有:
$$\begin{aligned} \left|\bigcup_{i=1}^n\overline{S_i}\right| &=\sum_{k=1}^n(-1)^{k-1}\sum_{a_{1,\cdots,k} }\left|\bigcap_{i=1}^{k}S_{a_i}\right|\\ &=\sum_{k=1}^n(-1)^{k-1}\dbinom{n}{k}(n-k)!\\ &=\sum_{k=1}^n(-1)^{k-1}\frac{n!}{k!}\\ &=n!\sum_{k=1}^n\frac{(-1)^{k-1} }{k!} \end{aligned}$$因此 的错位排列数为:
$$D_n=n!-n!\sum_{k=1}^n\frac{(-1)^{k-1} }{k!}=n!\sum_{k=0}^n\frac{(-1)^k}{k!}$$错位排列数列的前几项为 。
容斥原理模型
接着我们尝试抽象出容斥原理的模型:
-
全集 :不定方程 的非负整数解
-
元素:变量 .
-
属性:的属性即 满足的条件,即 的条件
目标:所有变量满足对应属性时集合的大小,即 .
这个东西可以用 $\left|\bigcap_{i=1}^{n}S_i\right|=|U|-\left|\bigcup_{i=1}^n\overline{S_i}\right|$求解。 |U| 可以用组合数计算,后半部分自然使用容斥原理展开。
那么问题变成,对于一些 的交集求大小。考虑 的含义,表示 的解的数目。而交集表示同时满足这些条件。因此这个交集对应的不定方程中,有些变量有 下界限制,而有些则没有限制。
能否消除这些下界限制呢?既然要求的是非负整数解,而有些变量的下界又大于 ,那么我们直接 演都不演了,把这个下界减掉,就可以使得这些变量的下界变成 ,即没有下界了。
因此对于$\left|\bigcap_{a_i<a_{i+1} }^{1\leq i\leq k}S_{a_i}\right|$的不定方程形式为
于是这个也可以组合数计算啦。这个长度为 的 数组相当于在枚举子集。
错位排列
bro以为容斥原理就这么结束了?哈哈,这个错位排列是假的,用来补全上述(以后认准 权威 字眼)。
容斥原理定义
编者注:下述理论很枯燥,看不懂别硬看,跳过或者直接记结论就好了
设 中元素有 种不同的属性,而第 种属性称为 ,拥有属性 的元素构成集合 ,那么
$$\begin{aligned}\left|\bigcup_{i=1}^{n}S_i\right|=&\sum_{i}|S_i|-\sum_{i<j}|S_i\cap S_j|+\sum_{i<j<k}|S_i\cap S_j\cap S_k|-\cdots\\&+(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^{m}S_{a_i}\right|+\cdots+(-1)^{n-1}|S_1\cap\cdots\cap S_n|\end{aligned}$$即
$$\left|\bigcup_{i=1}^{n}S_i\right|=\sum_{m=1}^n(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^mS_{a_i}\right|$$证明
对于每个元素使用二项式定理计算其出为
$$\begin{aligned} Cnt=&|\{T_i\}|-|\{T_i\cap T_j|i<j\}|+\cdots+(-1)^{k-1}\left|\left\{\bigcap_{i=1}^{k}T_{a_i}|a_i<a_{i+1}\right\}\right|\\ &+\cdots+(-1)^{m-1}|\{T_1\cap\cdots\cap T_m\}|\\ =&\dbinom{m}{1}-\dbinom{m}{2}+\cdots+(-1)^{m-1}\dbinom{m}{m}\\ =&\dbinom{m}{0}-\sum_{i=0}^m(-1)^i\dbinom{m}{i}\\ =&1-(1-1)^m=1 \end{aligned}$$于是每个元素出现的次数为 1,那么合并起来就是并集。证毕。
补集
对于全集 下的 集合的并 可以使用容斥原理计算,而集合的交则用全集减去 补集的并集 求得:
$$\left|\bigcap_{i=1}^{n}S_i\right|=|U|-\left|\bigcup_{i=1}^n\overline{S_i}\right|$$右边使用容斥即可。
错位排列
错位排列定义
错位排列(derangement)是没有任何元素出现在其有序位置的排列。即,对于 的排列 ,如果满足 ,则称 是 的错位排列。
例如,三元错位排列有 和 。四元错位排列有 和 。错位排列是没有不动点的排列,即没有长度为 1 的循环。
以上文字看不懂?回去种地吧(doge),开玩笑的。
不懂看一下生动的示例图。
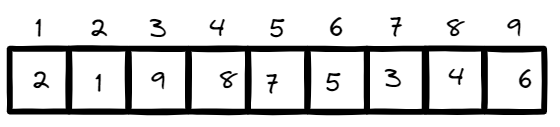
以上是合法的错位排列