看你们都在发博客，我也跟跟风吧

你们也看到标题啦，中缀表达式转前缀表达式在比赛常考，所以，我就来给你们补习补习

首先，我们要了解中缀表达式，其实中缀表达式是一种我们日常生活中最熟悉、最常用的数学表达式书写方式。它的核心特点是运算符（如 +, -, *, /）被放置在两个操作数（数字或变量）的中间。

而前缀表达式呢？它也称为波兰表示法或波兰表达式，是一种数学表达式的书写方式。它的核心特点是运算符被放置在两个操作数（数字或变量）的前面。

其实两种表达式在运算顺序和逻辑上没有什么不同，但是书写方法不一样

举两个很简单的例子：

你写1 + 1，这是中缀表达式，而前缀表达式是这样写的：+ 1 1，也就是把运算符号+、-、*、/放到两个运算的数前面而已啦

知道了这一点，那转换起来就很简单了吧！

比如这个：1+5/7*2,你能想出来吗？

你会说，不是哥们，你就教了这么点，谁不知道前缀表达式是“也就是把运算符号+、-、*、/放到两个运算的数前面而已啦”

那我告诉你怎么实践吧

刚刚那个表达式：1+5/7*2，我们可以把它拆成这么几个式子：5/7→*2→+1，也就是：[（5/7）*2]+1，按照我说的

“也就是把运算符号+、-、*、/放到两个运算的数前面而已啦”可得：

5/7→/ 5 7 将/ 5 7看做一个数字，之后就是用5/7的结果*2，即：* / 5 7 2,怕你们看不懂，其实它也就是：* ⁵/₇ 2

也是，两个数字的运算符放前面

知道了这点以此类推就是+ * / 5 7 2 1啦

可以直接看下表

前缀表达式、中缀表达式与计算结果对照表

前缀表达式 (Polish Notation)	等价中缀表达式 (Infix Notation)	计算结果	备注
+ 5 3	5 + 3	8	简单加法
- 9 4	9 - 4	5	简单减法
* 6 7	6 × 7	42	简单乘法
/ 15 3	15 ÷ 3	5	简单除法
+ + 2 3 4	2 + 3 + 4	9	连续加法
* * 2 3 4	2 × 3 × 4	24	连续乘法
- * 2 3 4	(2 × 3) - 4	2	混合运算1
/ * 4 5 2	(4 × 5) ÷ 2	10	混合运算2
* - 5 1 / 6 2	(5 - 1) × (6 ÷ 2)	12	混合运算3
- / 10 2 * 2 3	(10 ÷ 2) - (2 × 3)	-1	混合运算4
+ * 3 4 - 7 2	(3 × 4) + (7 - 2)	17	混合运算5
/ * + 1 2 3 4	((1 + 2) × 3) ÷ 4	2.25	嵌套运算1
+ - * 2 3 4 / 6 2	(2 × 3 - 4) + (6 ÷ 2)	5	嵌套运算2
* + 1 2 + 3 4	(1 + 2) × (3 + 4)	21	嵌套运算3
- + * 2 3 4 / 10 5	(2 × 3 + 4) - (10 ÷ 5)	8	复杂嵌套
+ / * 5 6 2 - 8 3	(5 × 6 ÷ 2) + (8 - 3)	20
* - / 15 3 2 + 1 4	(15 ÷ 3 - 2) × (1 + 4)	15
+ + + 1 2 3 4	1 + 2 + 3 + 4	10	多重连续
- - - 20 5 3 2	20 - 5 - 3 - 2

前缀表达式求值规则：

1. 从右向左扫描表达式
2. 遇到操作数则压入栈中
3. 遇到运算符则弹出栈顶两个操作数进行计算
4. 将计算结果压回栈中
5. 重复上述步骤直到表达式最左端
6. 栈中最后的元素就是最终结果

示例： 计算 - * 2 3 4

1. 扫描 4 → 压栈: [4]
2. 扫描 3 → 压栈: [4, 3]
3. 扫描 2 → 压栈: [4, 3, 2]
4. 扫描 * → 弹出 2 和 3 → 计算 2*3=6 → 压栈: [4, 6]
5. 扫描 - → 弹出 6 和 4 → 计算 6-4=2 → 压栈: [2]
6. 结果: 2

学废了记得感谢我哦

第一次写博客可能质量很差，其他大佬请指教哈

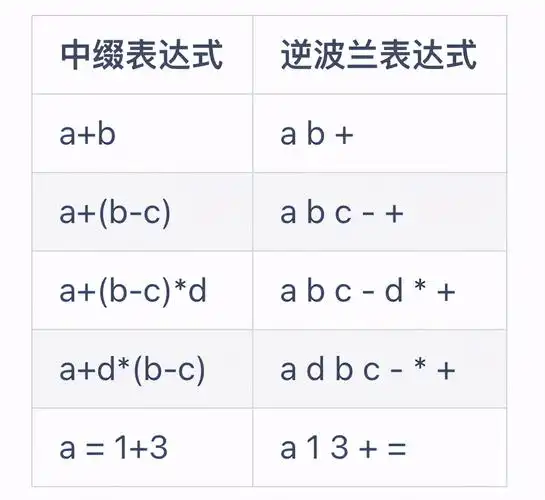
这是后缀表达式，也就是逆波兰式表达式其实和前缀表达式原理一样的啦