背景

D老师要变法了，竟然让我们做笔记！！！不过我做了……

---

动态规划是……额（别管，反正我有重要的东西）。

动态规划有三点特征：

1. 无后效性
2. 最优子结构
3. 重叠子问题

特征

1. 无后效性

用求斐波那契数列来举例。

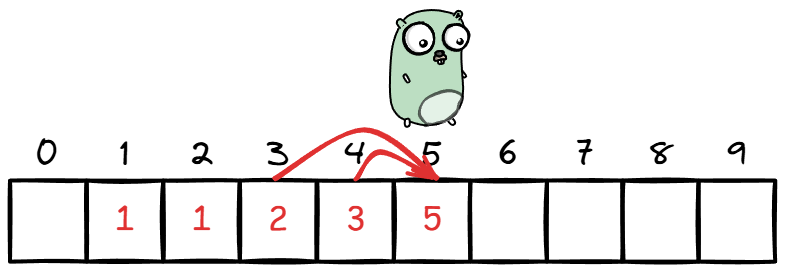
在求 fib 时小拨鼠一直往前走，且每一项只与前两项关联，不会——用 D 老师的话来说——算着算着突然到前面把一个数字的答案改了。

其实下面这个特征没听懂，只好从字面理解一下。

2. 最优子结构

可能类似贪心，每次解决子问题时都选取最优的答案，从而保证整个结果的答案最优。

3. 重叠子问题

这个比较好理解。和分治有点像，动态规划也是把一个问题转化成几个重叠的子问题，逐一求解，再把子问题的解拼接起来。得到整个问题的最优解。图示：

怎么感觉怪怪的？

---

解题思路

其实动态规划和递推很类似。翻了一下前面递推的解题思路，竟然和动态规划一模一样！

下面是步骤（都是动宾短语耶）：

1. 分析问题
2. 定义状态变量
3. 设计状态转移方程
4. 设置初始状态和边界
5. 确定答案

1. 分析问题

分析问题，就是分析这道题能不能用动态规划来做。

但是这里要说的是动态规划的解决方法。既然解题步骤都和递推一样，那么解题方法肯定是可以用递推来做的。还是用求斐波那契数列来举例。这个都会吧？下面是核心代码：

f[] = {0};
f[1] = f[2] = 1;
for (int i = 3; i <= n; i++)
{
	f[i] = f[i - 1] + f[i - 2];
}
cout << f[n];

时间复杂度： $O(n)$ 。

很容易联想到这个也能用递归来解。其实也说明了动态规划是可以用递归来解的，因为它和分治类似，都是分解子问题。下面是递归的核心代码：

int fib(int x)
{
	if (x == 1 || x == 2)return 1;
	return fib(x - 1) + fib(x - 2);
}

但是由于子问题是重叠的，而且（如图）求第 6 项的时候已经求过第 4 项了，在求第 6 项的第二个分支（即第 5 项）的时候不需要再求一遍了。

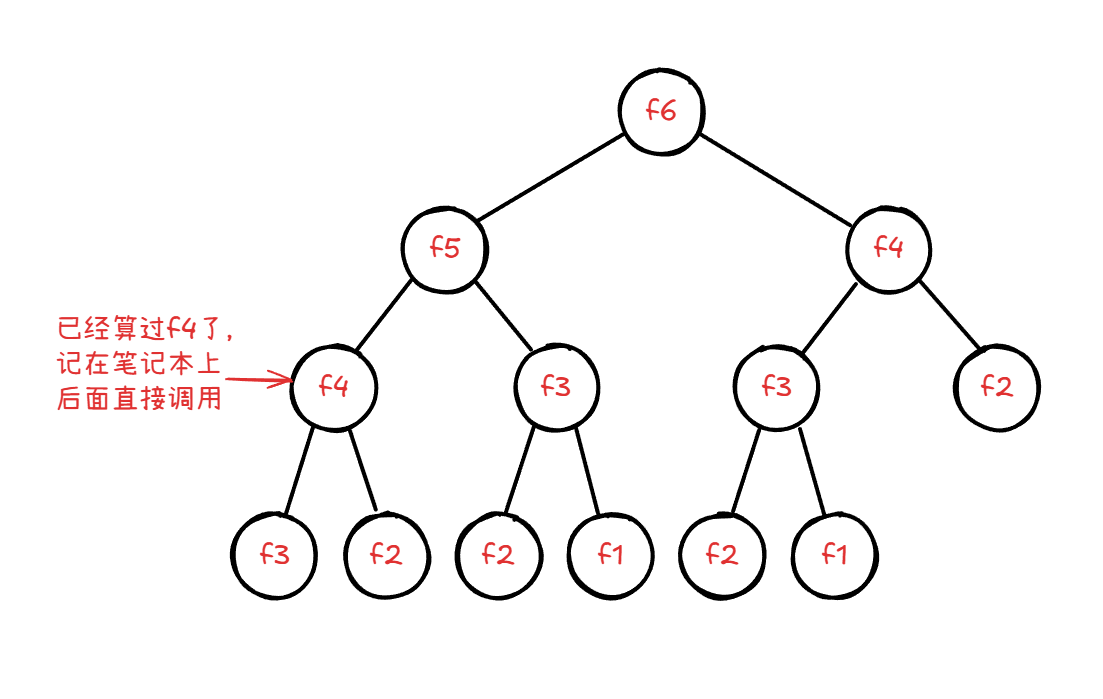
这就要考虑记忆化剪枝。以下是记忆化剪枝的核心代码：

int f[N];
int fib(int x)
{
	if (x == 1 || x == 2)return 1;
	if (f[x])return f[x];
	return f[x] = fib(x - 1) + fib(x - 2);
}

经过优化后，递归写法也可以优化到将近 $O(n)$ 的时间复杂度。

2. 定义状态变量

状态，就是小拨鼠在计算这一项的状态。而变量，就是和这一状态相关的变量。既然使用递推（即填表法）的方法求动态规划，那就需要一张表。怎么得到这张表呢？就需要关系到状态变量了。最简单的方法就是多少变量就定多少维。 但这太浪费了，我还有一个序号 $i$ 呢。 这一步就是设计表格（表的每一格表示的意思）。用求 fib 举例。很明显，可以发现与当前状态相关的变量只有两个：序号 $i$ 和当前值 $S_i$ 。因此，关于求 fib 的表只需要 1 维就够了。其实判断要怎么设计表格也有技巧（用求 fib 举例）：

1. 从问题出发。问题是：求斐波那契数列的第 $n$ 项？ ；
2. 把问题转化为数学公式： $f(n)=?$ ；
3. 答案就是 $f[n]$ ；
4. 转化成通式： $f[i]=S_i$ 。

由此就能得到设计的表格。

3. 设计状态转移方程

可以把它想象成（其实就是）填表的方法。这样想就会容易得多：我从哪里来？我要到哪里去？

用求 fib 为例：求 fib 的状态转移方程就是：

$$f[i] = f[i - 1] + f[i - 2]$$

4. 设置初始状态和边界

这无非就是几种可能：

1. 全部都为最小值或最大值；
2. 全部都与输入相同；
3. 第一项与输入相同；
4. 前几项为已知值。

用求 fib 举例，初始状态就是 f[N] = {0}，边界就是 f[1] = f[2] = 1 。

5. 确定答案

这也只有几种情况：

1. 数组的第 $n$ 项；
2. 数组的最大或最小值；
3. 数组所有数的和。

用求 fib 举例，答案就是 f[n]。

---

D 老师给我们上传文件图片的权限吧，每次都要截图、保存、上传到 luogu 太麻烦了。再说， luogu 也是要空间的。