- gf24240 的博客
《梦溪笔谈·笔记》2025/7/19:区间DP
- @ 2025-7-19 22:01:34
说明
完了,区间 DP 太难了……(在学背包 DP 前我也是这么说的)只好讲的机械一点了。
这篇笔记分为区间分割和区间合并
上面就说过了,区间 DP 分为 区间分割 和 区间合并
区间 DP - 区间分割
区间分割的意思是:有一段区间(或者 个数或一段线性序列),需要分为 个部分,每部分有权值(就是类似价值或答案),求如何分割区间,使权值最优。
一、分析问题
反正我看不出动态规划的特征。也许有最优子结构(前 i - 1 部分最有,那前 i 部分也最优)。
二、定义状态变量
从问题出发。问题: 个数字分成 个部分的最大权值。
定义 dp[i][j] 表示前 个数字,分成 个部分的最大权值。
三、状态转移方程
需要用两个循环来枚举 和 。直接枚举到 和 就好了。
如图:
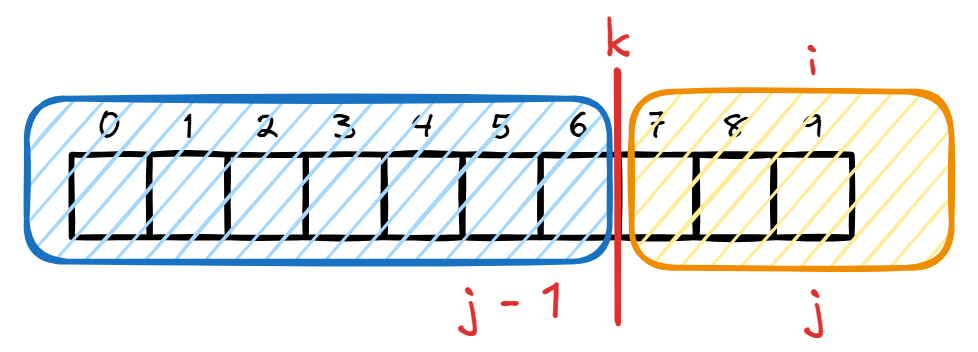
( 应该是上图 的前面一格。其实右边一格也可以)
可以模拟一个断点 (注意是小写,和上面的 不一样),把这 个数分成两部分。拆分之后的权值就是 dp[k][j - 1]+j的权值 (分割前 个数为 部分)。跟原来的权值比较,如果更优,则更新。
先上张大图:
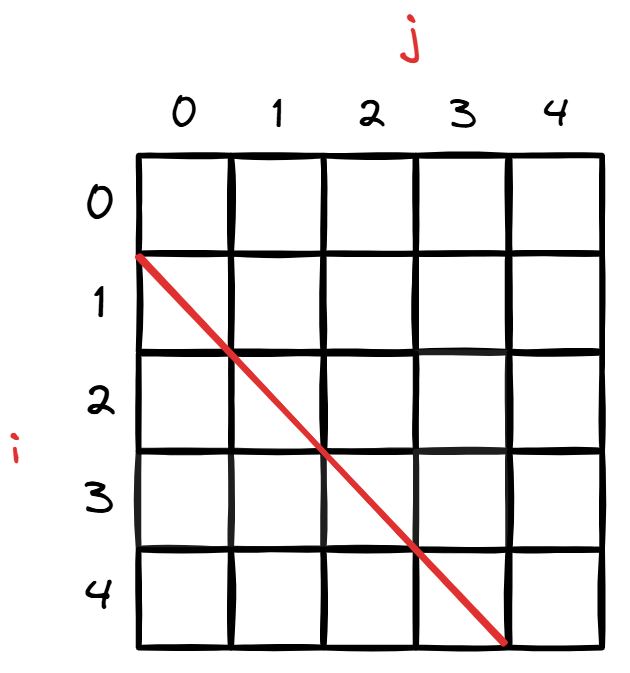
根据上面的定义,可以很快发现,红线(对角线, 和 相等)的上方(不包括红线)的值是无效的。因为:例如 ,三个数不可能分割成七部分。但是可以循环到 ,只是这个值无效而已。
断点的区间
这也是一个问题。我们不可能把断点从 到 一直循环吧。这里有最右和最左两个情况。
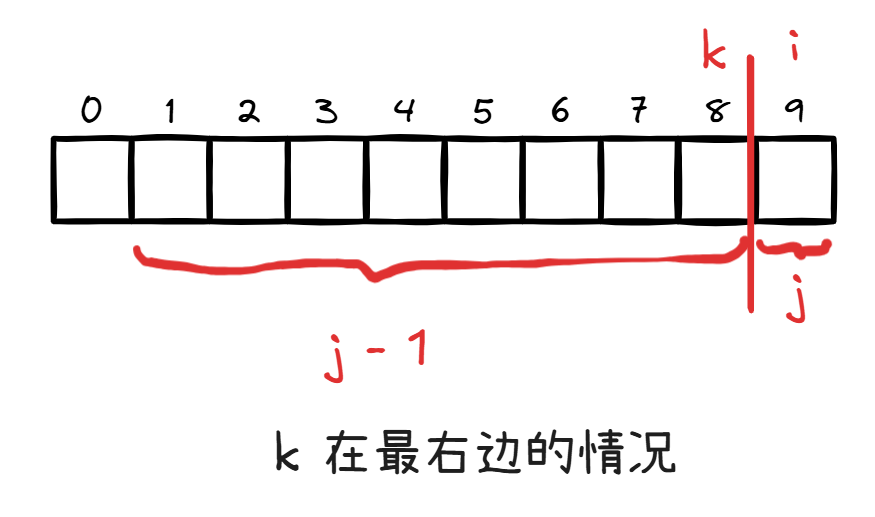
这是最右边的情况,至少 有一个格子。(这时 )即
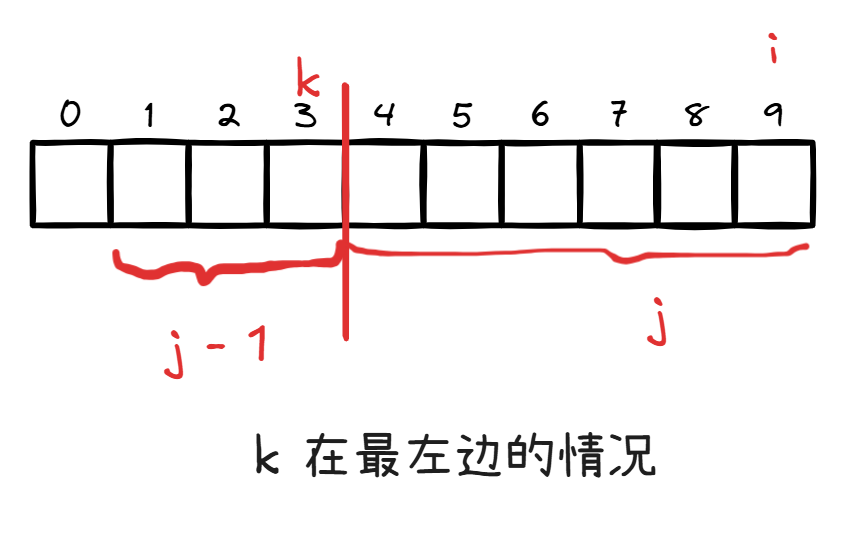
这是最左边的情况,在 左边至少有 个数。即 。
于是就有了断点 的取值范围: 。如图:
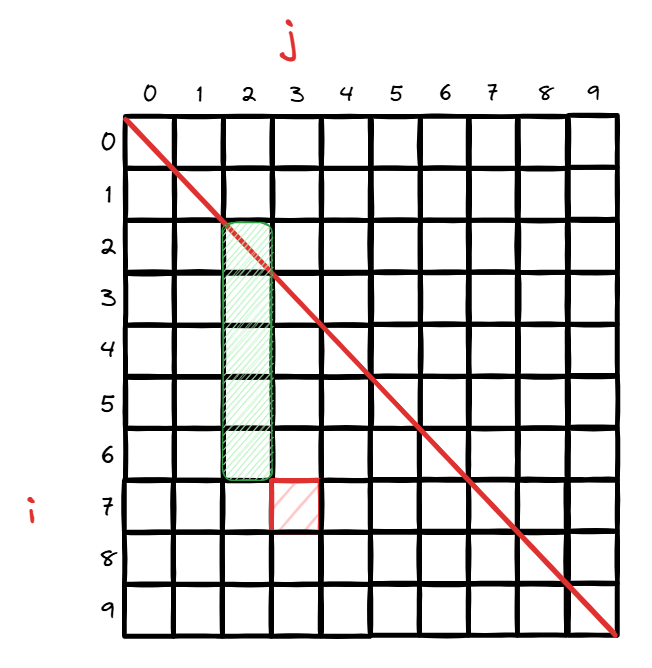
图中绿色格子就是 的范围。
四、初始状态和边界
求边界值,只需要把当前状态推到最前,看看与它的相关状态知不知道,能不能求出当前状态。
区间分割的初始状态一般在第 行或(和)第 列。
五、答案
前 个数,分割成 部分,即 dp[n][k] 。
核心代码:
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= K; j++)
{
for (int k = j; k < i; k++)
{
dp[i][j] = max/min(dp[i][j], dp[k][j - 1] + w[k + 1][i]);
}
}
}
例题:乘积最大
区间 DP - 区间合并
这部分就比较好理解了。不过我还是讲集训的格式吧(只因 D 老师讲的听不懂)。
区间合并的意思是:有 段区间,可以合并一些区间,产生价值。求如何合并区间,使最终价值最大。
一、分析问题
- 无后效性: 这是真看不出来;
- 最优子结构: 前 段价值最大,那前 段的价值也会最大;
- 子结构重叠: 小区间和大区间当然是重叠的。
二、定义状态变量
- 看到这个问题,在结合上面的区间分割,你是不是想到了定义
dp[i][j]表示前 个区间,合并成 个区间的最大价值?其实不是的。 - 从问题出发。问题:整个区间(即 )的最大价值;
- 转换为通式: ;
- 转换为数组:
dp[i][j] = Sij; - 状态变量:
dp[i][j]表示区间 的最大价值。
三、状态转移方程
以上的内容都是和 D 老师写法一样的。下面就不一样了。
集训写法
首先肯定要模拟区间。这里使用一个 len 循环模拟区间的长度。这个变量需要从小到大循环(如果从大到小的话就会造成计算大区间时小区间未计算)。再用一个循环枚举起点 s 。这样终点 e 就可以计算出来,即 。
和区间分割一样,需要模拟断点。和区间分割不同的是,区间合并的有效数据是在红线(对角线)的上方。例如区间 ,这是不合法的。
模拟这个断点有什么用呢?不知道。也许是通过断点 来合并 和 。好像写了这么多也没说到重点。
这也和区间分割差不多。把区间 分成 和 ,加上合并价值。取较优值。
D 老师写法
其实我没听太懂。不过大概还是知道的,而且我还会重新看的。
模拟断点 是一样的。区别是模拟起点和终点。不过要注意区间长度要从小到大,避免上面的问题。
四、初始状态和边界
初始值就是最大值就定义最小,最小值就定义最大。
边界一般是对角线(即区间长度为一)。
五、答案
区间 ,即 dp[1][n] 。
