前言

想来想去还是“前言”好一点。

说实话我一直不直到这个算法的名字。以后就叫它倍增了。以下的倍增均指我们目前学的倍增（也不知道后面有没有其他倍增）。

---

描述

其实这是提高组的内容。放在这只是因为有点像 DP 而已。

倍增就是成倍增长（有点像反过来的二分）。例如我这次计算 $i$ 个，下一次计算 $i*2$ 个，再下次计算 $i*2^2$ 个。

倍增一般是：一段序列 $A$ ，有 $Q$ 个询问，每次询问包含起点和终点，求在序列 $A$ 中起点到终点的最大 / 最小值。

既然有点像动规，就用动规的思路来解决吧。

一、分析问题

1. 无后效性： 额……反正不是动规；
2. 最优子结构： 每段区间的值最优；
3. 重叠子问题： 区间是重叠的。

二、定义状态变量

联想到区间动规，你是不是想到：定义 dp[i][j] 表示区间 $[i,j]$ 的最小值（这里用最小值来举例）？其实不是的。

这里定义 f[i][j] 表示区间 $[i, i + 2^j - 1]$ 的最小值，即从 $i$ 开始数 $2 ^ j$ 个数的最小值。

三、状态转移方程

可以把中间的点看成断点。一半的数就是 $2^{j-1}$ 。而前一半的最小值就是 f[i][j - 1] 。那后一半呢？首先个数肯定也是 $2 ^ {j-1}$ 。那起点不就是 $i + 2^{j-1}$ 嘛。取较小值，就是 f[i][j] 的答案。即：

$$f[i][j] = min(f[i][j-1],f[i+2^{j-1}][j-1]);$$

那 $i$ 和 $j$ 的范围呢？

算了，直接看模板吧，我也不知道怎么讲。

for (int j = 1; j <= Log[n]; j++)
{
	for (int i = 1; i + (1 << (j - 1)) <= n; i++)
	{
		f[i][j] = min(f[i][j - 1], f[i << (j - 1)][j - 1]);
	}
}

不过我是知道 $i$ 的范围的。如图：

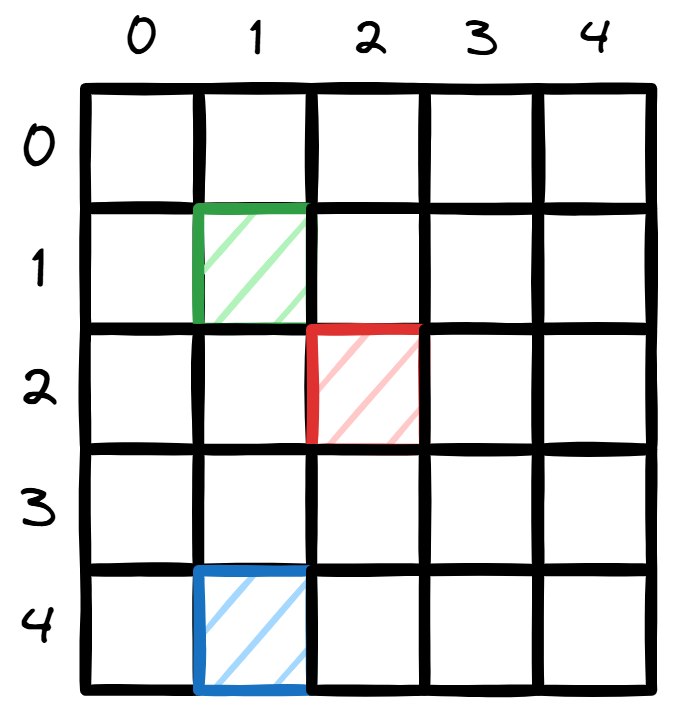
红色的格子是由绿色和蓝色（当然这蓝色格子不准确）格子转移而来。只需要保证这些格子不出界就好了。 $j$ 自然就是 $\log{n}$ 。而 $i$ 需要保证 $i + 2^{j-1}$ （蓝色格子）不超过 $n$ 。

四、初始状态和边界

• 初始状态：从任意一个 $i$ 开始数一个数都是 $a_i$ 本身。即 f[i][0] = a[i] 。
• 边界：上面就是了。

五、答案

这就有点困难了。询问区间 $[l,r]$ 总不能直接用 f[l][r] 吧？设 f[l][x] 为答案。先上张大图：

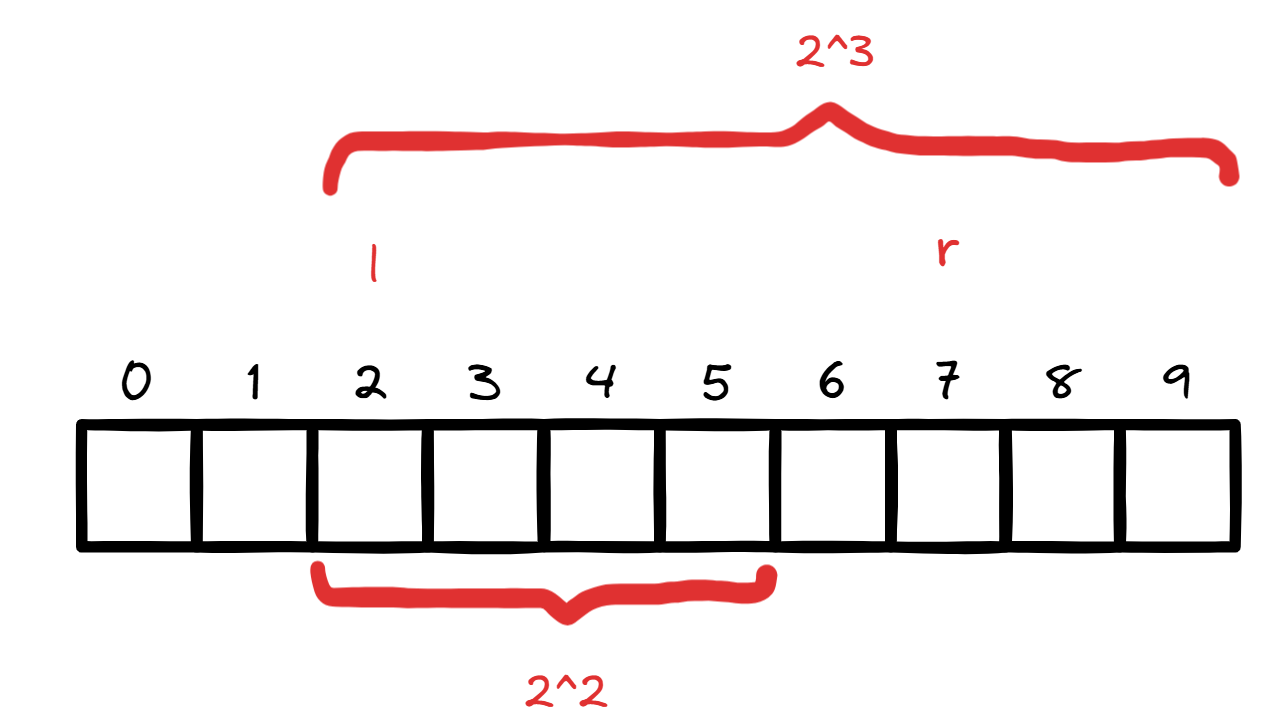
要求这个区间，首先就要找到 $x$ 表示的数。可以发现，这首先就要求 $2$ 的多少次方是 $r-l+1$ （ $r$ 和 $l$ 之间的数字数）。但是要找到精确的数几乎不可能，毕竟数组下标也只有整数。上图中很容易看出这个数是 $3$ 。但是这也不全面，如果剩下的格子里有更小的数呢？

这里可以这样：

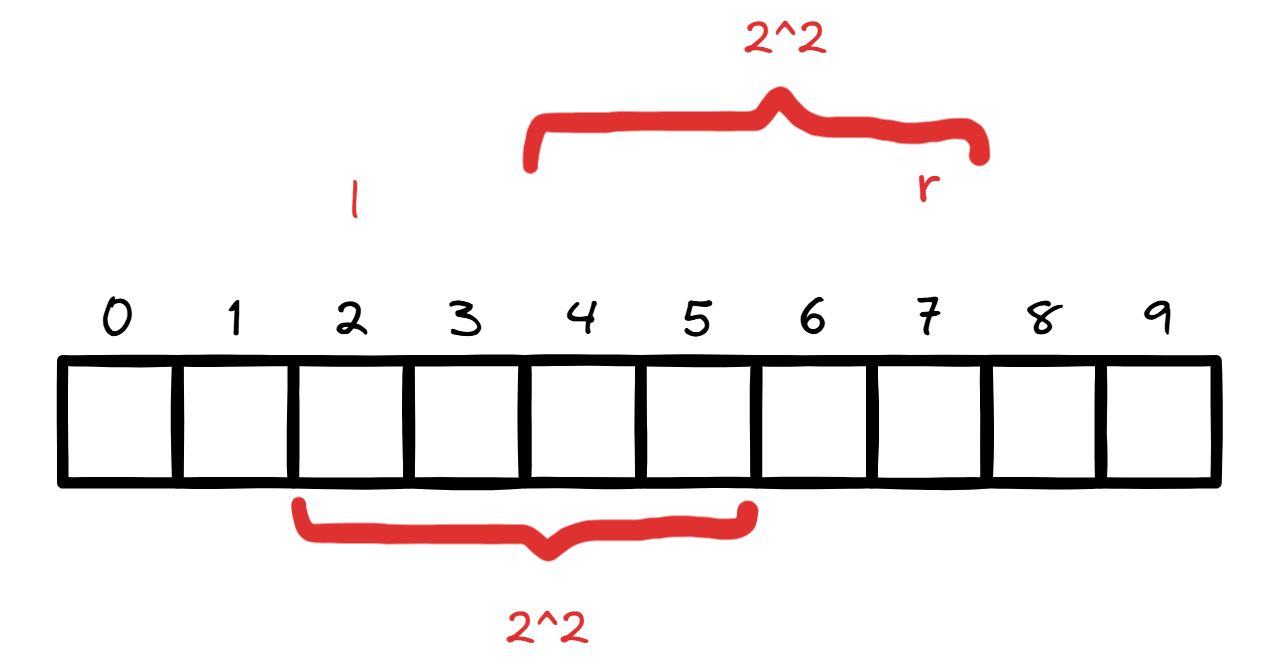
从 $r$ 开始从后往前再数 $2^3$ 个数。这样就能包括所有数，而又不多出来。但是我们的数组是从前往后数的，而不是从后往前。那就需要找到这个往前数的起点了。很显然是 $r - 2^x + 1$ 。

那这个 $x$ 怎么求呢？用二分吗？这也是一个思路。但是二分的效率还是太低了，我们需要 $O(1)$ 的时间复杂度。要求 $2$ 的多少次方是 $x$ ，很容易想到 $\log_2$ 函数。于是就有了： $x=\log(r-l+1)$ （应该默认是 $\log_2$ 吧）。

但是 cmath库中 log() 函数效率不够高，需要优化（这是 D 老师讲的，我感觉效率挺高的）。可以考虑： $\log{n} = \log{\frac{n}{2}} + 1$ 。使用数组存储。于是就得到了倍增 ST 表的模板：

#include <iostream>
using namespace std;

const int N = 25005;
int n, a[N], f[N][50], m, Log[N];

int main()
{
    cin >> n >> m;
    Log[0] = -1;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        f[i][0] = a[i];
        Log[i] = Log[i >> 1] + 1;
    }
    for (int j = 1; j <= Log[n]; j++)
    {
        for (int i = 1; i + (1 << j) - 1 <= n; i++)
        {
            f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
        }
    }
    for (int i = 1; i <= m; i++)
    {
        int l, r;
        cin >> l >> r;
        int k = Log[r - l + 1];
        cout << min(f[l][k], f[r - (1 << k) + 1][k]) << "\n";
    }
    return 0;
}

剩下就靠思维了。