说明

我也想讲详细一点，但可惜详细的原版不幸丢失，只好写得像数学书一样简洁了。这是重制版。

---

图的简单概念和分类

概念：由点和边组成的二元组。例如这是一个图：

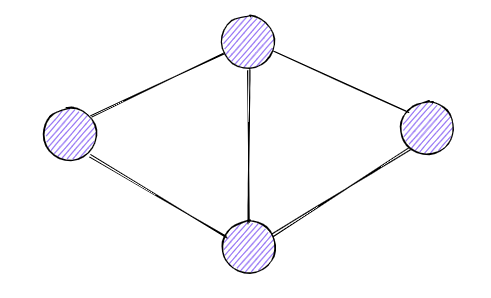
分类：

---

图的存储和遍历

这有三种方式：

1. 邻接矩阵；
2. 链接矩阵；
3. 前向星；

邻接矩阵

如图：

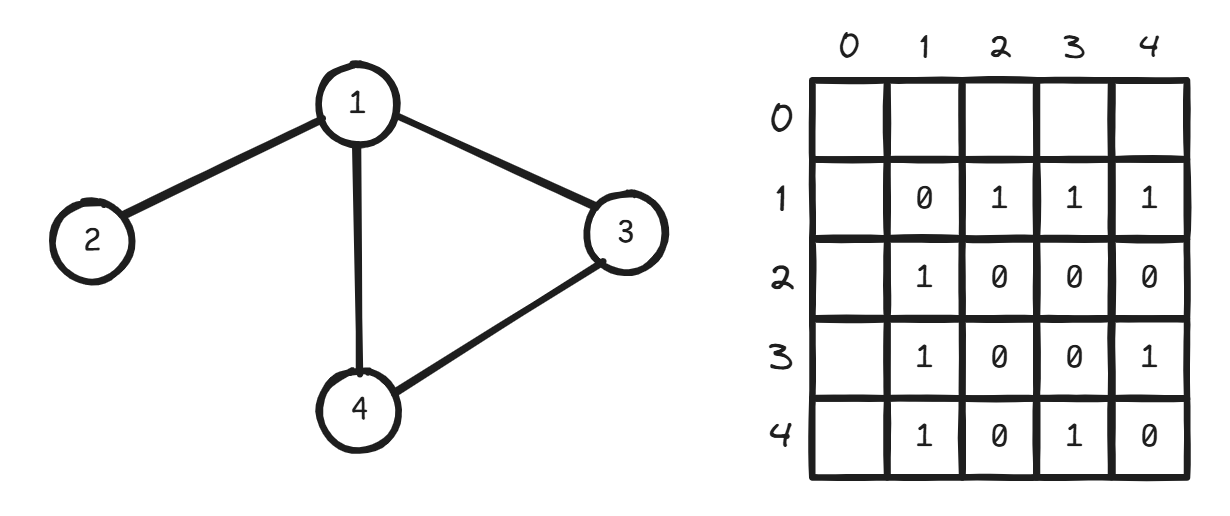
使用二维数组存储节点之间的关系，可以是权值或 $0$ 。图的遍历可以使用搜索的方式。核心代码：

void dfs(int u)//深搜遍历
{
    cout << u;
    for (int v = 1; v <= n; v++)
    {
        if (g[u][v] == 1 && !vis[v])
        {
            vis[v] = 1;
            dfs(v);
        }
    }
}

void bfs()//广搜遍历
{
    queue <int> q;
    q.push(1);
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        cout << u;
        for (int v = 1; v <= n; v++)
        {
            if (g[u][v] == 1 && !vis[v])
            {
                vis[v] = 1;
                q.push(v);
            }
        }
    }
}

cin >> n >> m;
for (int i = 1; i <= m; i++)//存储
{
    int u, v;
    cin >> u >> v;
    g[u][v] = g[v][u] = 1;
}

链接矩阵

其实这是我自己起的名字。它叫邻接链表，用链表来存储每一条边。但是使用 vector 更方便。如图：

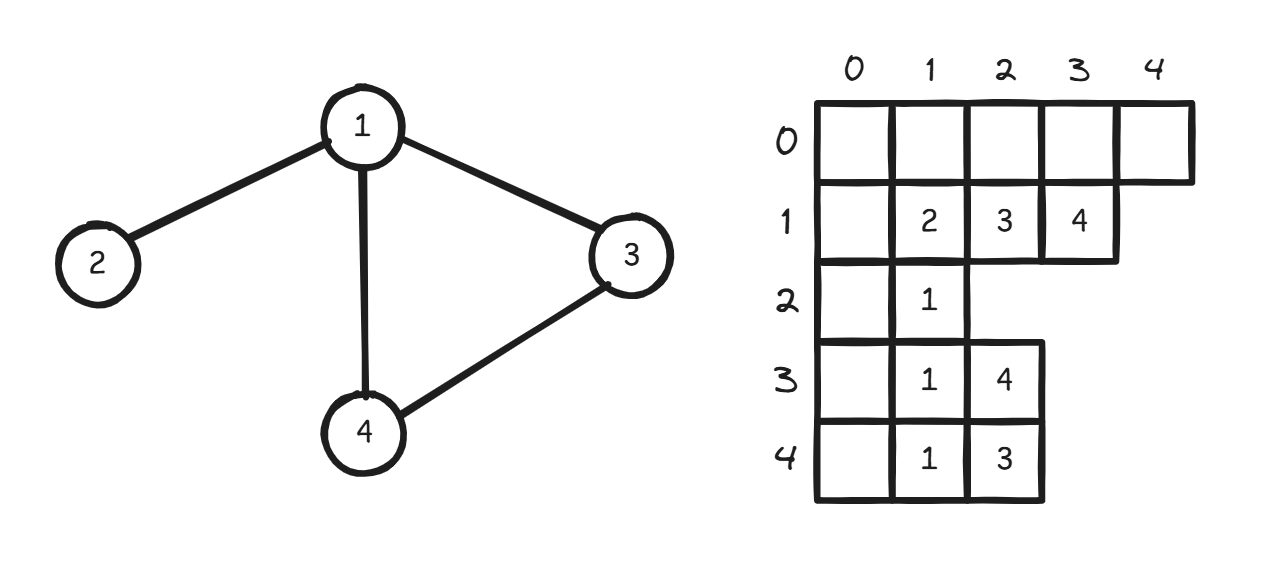
用 vector 动态分配内存的特点。每一行存储的是与当前节点连接的节点。遍历相似。核心代码：

void dfs(int u)//深搜遍历
{
    cout << u;
    for (auto v : g[u])
    {
        if (!vis[v])
        {
            vis[v] = 1;
            dfs(v);
        }
    }
}

void bfs()//广搜遍历
{
    queue <int> q;
    q.push(1);
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        cout << u;
        for (auto v : g[u])
        {
            if (!vis[v])
            {
                vis[v] = 1;
                q.push(v);
            }
        }
    }
}

cin >> n >> m;
for (int i = 1; i <= m; i++)//存储
{
    int u, v;
    cin >> u >> v;
    g[u].push_back(v);
    g[v].push_back(u);
}

前向星

这里讲讲概念，也就算了。前向星就是静态链表。你需要准备这些：

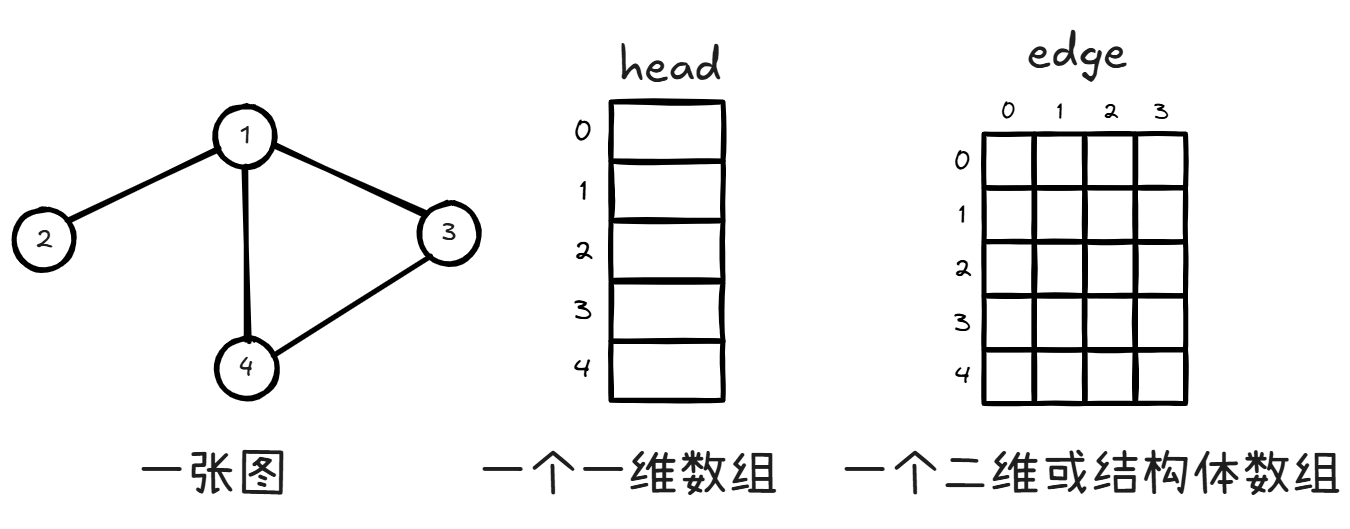
• 一张图：用来用；
• 一个一维数组：存储每条边的头节点；
• 一个二维数组：每行包含三个量： $u$ 、 $v$ 和 $next$ 。$u$ 和 $v$ 用来存储连接的两个节点。 $next$ 用来存储与 $u$ 节点连接的下一条边。

遍历：从 $head_u$ 开始，下一条边即为 $edge[u].next$