前言

之所以叫树论是因为这篇 blog 理论知识较多。

---

树

树是一棵树。

树是一种联通、无向图。节点不成环。例如这是一棵树：

• 在最上面的节点是 根节点 ；
• 连接节点的线叫 边 （同图）；
• 树的 $节点数 = 边数+1$ ；
• 节点下面的节点叫 子节点 ，这个节点叫这些节点的 父节点 ；
• 有子节点的节点叫 分支节点 ，无子节点的节点叫 叶子节点 ；
• 该节点的子节点数叫做这个节点的 度 ，整棵树的度为每个节点的最大度；
• 每个节点到根节点的距离叫做 层 或 深度 ；

二叉树

二叉树是一种树。它的度为二，即每个节点最多有两个子节点。例如这是一个二叉树：

注意 ：二叉树不一定每个分支节点都有两个子节点。

满二叉树和完全二叉树

• 满二叉树： 除叶子外，所有节点都有 $2$ 个子节点。
• 完全二叉树：除最后一层的节点从左往右排列，所有层都有 $2^{i-1}$ 个节点。

二叉树的性质

1. 性质一： 若根节点的深度为 $1$ ，则第 $i$ 层的节点树最多为 $2 ^ {i - 1}$ 个；
2. 性质二： 深度为 $k$ 的二叉树节点数最多为 $2 ^ k - 1$ ；
3. 性质三： 定义叶节点个数为 $n_0$ ，度为二的节点数为 $n_2$ ，则 $n_0 = n_2 + 1$ ；
4. 性质四： 有 $n$ 个节点的完全二叉树深度必为 $\lfloor \log_2{n} \rfloor + 1$ ；

树的存储

树的存储有两种：

1. 顺序存储；
2. 链式存储；

顺序存储 的三种方法：

1. 父亲表示法：数组存储该节点和该节点的父节点；
2. 孩子表示法：数组存储该节点的该节点的孩子节点；
3. 父亲孩子表示法（可以叫家庭表示法）：数组存储该节点、父节点和孩子节点。

链式存储 的两种方法：

1. 孩子链表表示法：对于每个节点，都用一条链表连接该节点的每一个孩子节点；
2. 孩子兄弟表示法：转换成二叉树，在用双指针链表（或二叉链表，都是我自己起的）存储。（具体如下）

二叉树的存储优化

通过观察，发现二叉树的任意一个节点的父节点为 $\lfloor i / 2 \rfloor$ ，左儿子为 $2i$ ，右儿子为 $2i+1$ 。因此可以定义一维数组，下标表示节点编号。

不规则树转二叉树

不规则树转二叉树可以使用孩子兄弟表示法。秘诀： 长子当左儿子，兄弟关系向右斜。例如这个不规则二叉树：

还原

只需要倒过来。

二叉树的遍历

二叉树的遍历有四种方法：

1. 前（先）序遍历：根节点——左儿子——右儿子；
2. 中序遍历：左儿子——根节点——右儿子；
3. 后序遍历：左儿子——右儿子——根节点；
4. 层次遍历（即 BFS ）；

例如这个二叉树：

根据遍历还原二叉树

还原二叉树可以根据前或后序遍历之一和中序遍历结合得到唯一二叉树。只有前序和后序遍历不能还原唯一二叉树。 方法（以前序遍历为例，后序遍历只需倒过来）：

1. 先拿出前序的第一项，设为d
2. 找到中序遍历中d的位置
3. 在左边的为左儿子，反之为右儿子
4. 递归下去

如果是前序和后序，只能确定分支节点的顺序，不能确定叶节点的顺序。

哈夫曼树

哈夫曼树，是用来编哈夫曼编码的树。哈夫曼编码采用贪心思想， 出现次数越多，编码越短。例如这一题：

7.【NOIP2011】现有一段文言文，要通过二进制哈夫曼编码进行压缩。简单起见，假设这段文言文只由4个汉字“之”、“乎”、“者”、“也”组成，它们出现的次数分别为700、600、300、200。那么,“也”字的编码长度是( )。

1. 1
2. 2
3. 3
4. 4

答案：3 。

步骤：

1. 计算每一个字符出现的次数，根据次数排序；
2. 每次拿出出现次数最小的，合并权值；
3. 然后就得到了哈夫曼树；
4. 根据根节点到每一个节点的路径确定编码。

例如上题：

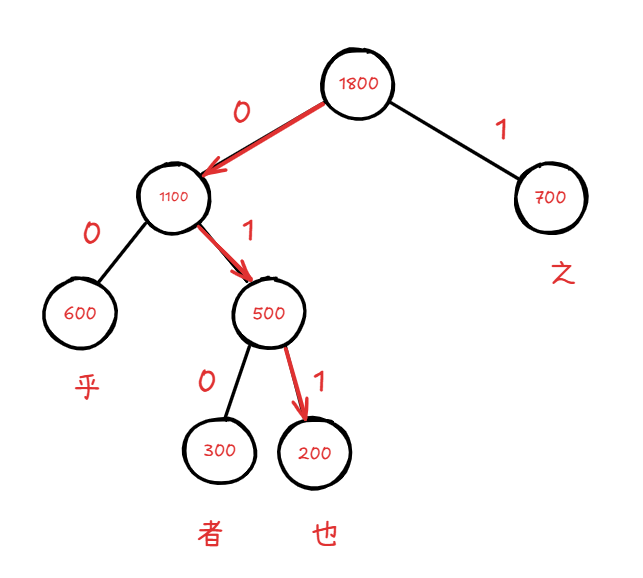
• “之”编码： 1 ；
• “乎”编码： 00 ；
• “者”编码： 010 ；
• “也”编码： 011 ；
• “之乎者也”编码： 100010011 ；

哈夫曼编码有两个特性：

1. 所有编码中最短 ；
2. 无二义性；

无二义性，即一串编码不可能解译两种及以上种意思。因为哈夫曼编码不可能有一个编码是另一个字符的前缀。有上图可以发现，所有字符在哈夫曼树中都是叶子节点，所以没有一个字符会在另一个字符回到根节点的路上。