前言

终于励志要写笔记了。本片 blog 理论部分较多。

---

整除

整除的定义

对于任意整数（至少我认为是这样的） $a$ 和 $b$ ，如果存在一个整数 $q$ 使 $b \times q = a$ 成立，则称 $b$ 整除 $a$ ，记作 $a|b$ 。且称 $a$ 是 $b$ 的倍数， $b$ 是 $a$ 的因数。

整除的性质

这不是那么容易记住的。

1. 如果 $a|b,b|c$ ，那么 $a|c$ 。
2. $a|b$ 而且 $a|c$ 等价于对于任意整数 $x$ 和 $y$ ，有 $a|(b \times x + c \times y)$ 。
3. 设 $m \neq 0$ ，那么 $a|b$ 等价于 $(m \times a)|(m \times b)$ 。
4. 设整数 $x$ 和 $y$ 满足 $a \times x + b \times y = 1$ ，且 $a|n$ $b|n$ ，那么 $(a \times b)|n$ 。
5. 若 $b=p \times d + c$ ，那么 $d|b$ 的充要条件是 $d|c$ 。

一道例题： 教堂 。

参考题解： 原文

---

鸣谢： @ 提供思考。

死板题解：本题考虑 $m$ 和 $n$ 的奇偶性。

#include <iostream>
using namespace std;

int m, n;

int main()
{
    scanf("%d %d", &m, &n);

    if (n == 1 || m == 1)
    {
        printf("%.2lf", (m + n - 2) * 2.0);
    }
    else if ((n * m) % 2 == 0)
    {
        printf("%.2lf", 1.0 * (n * m));
    }
    else
    {
        printf("%.2lf", (n * m - 1) + 1.414);
    }
    return 0;
}

不过不看题解谁能想到呢？

还是回到死板题解上来。

这道题的关键是这一点：如果要找到从原点出发经过全部点回到原点，需要尽量少走重复的点，而为了少走重复的点，就需要把全部点拉成一条线。分三种情况：

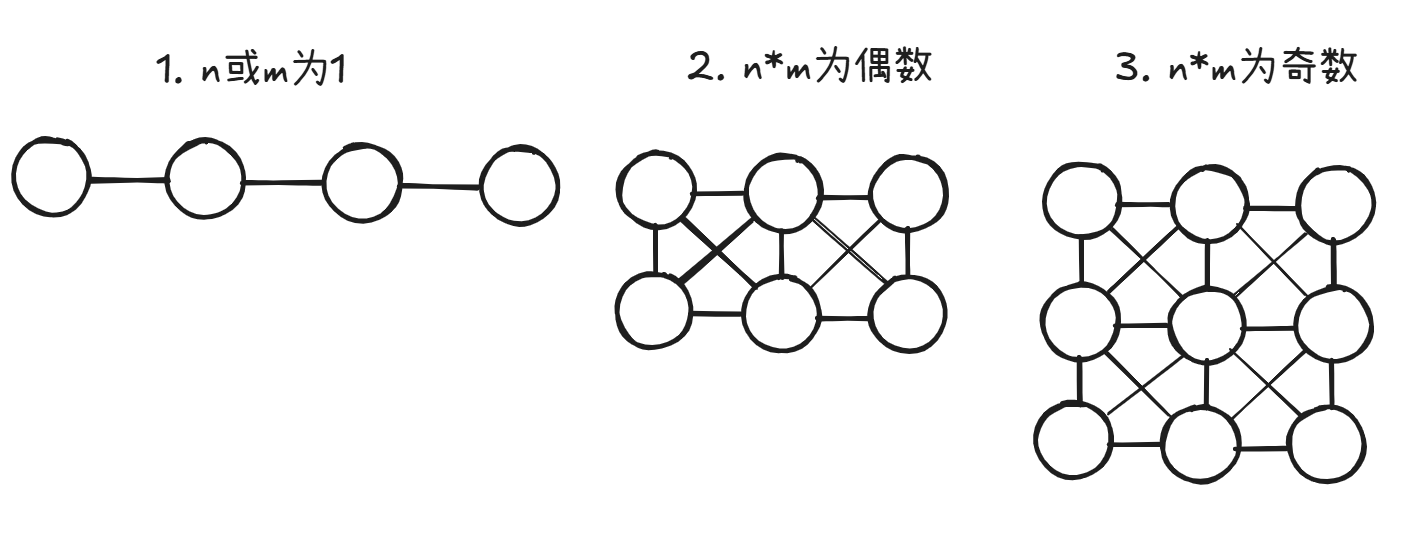
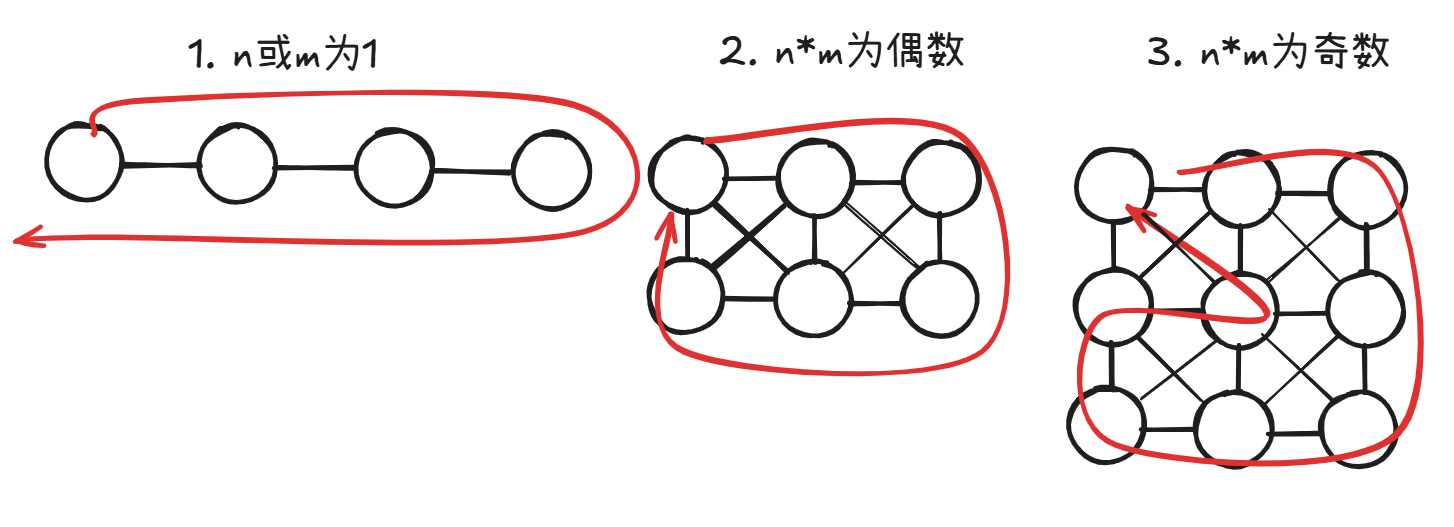
而这三种情况的路线是：

第一种情况： 这本来就是一条线了，最短的路径只有走到头再走回来。路径： $n(或m) \times 2 - 2$ 。

第二种情况： 这很显而易见。如果把所有点拉成线，最后终点和起点是直接相连的。所以路径就是点数，即 $n \times m$ 。

第三种情况： 这需要详细的讨论。把所有点编号，再拉成线。如图：

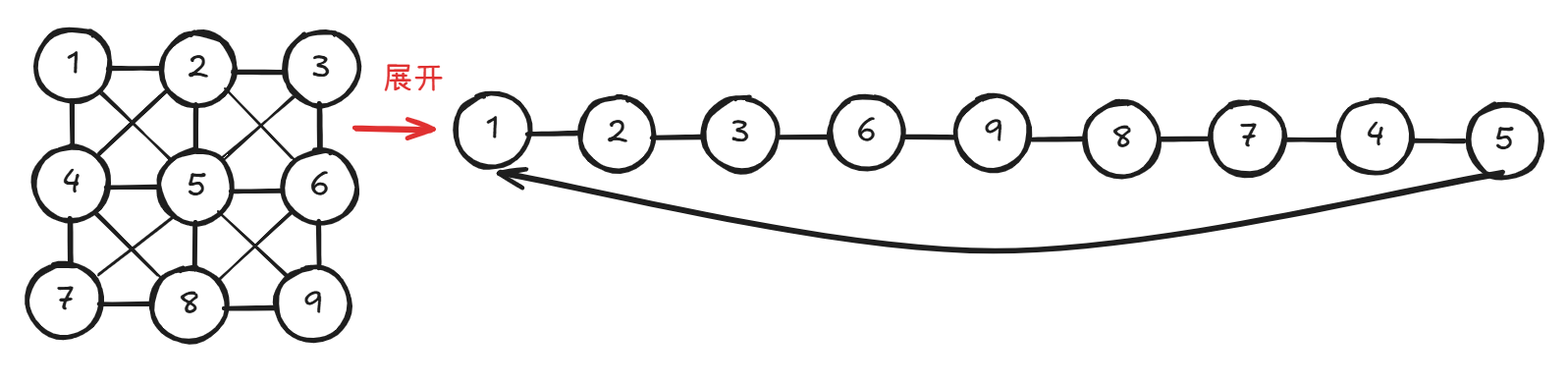
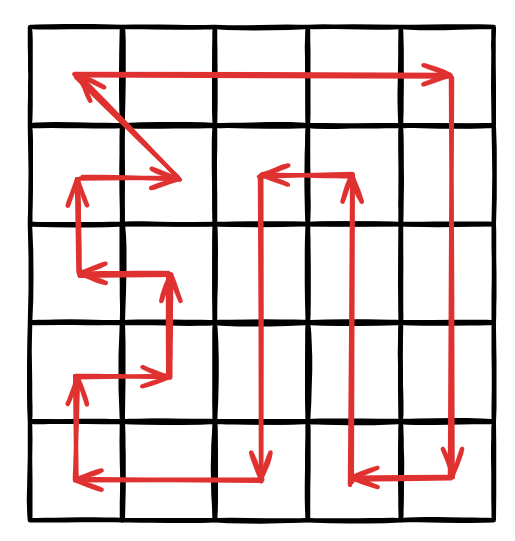
前面全部点都能拉成线，而最后一个点和起点由一点对角线相连。路径： $n \times m - 1 + 1.414$ 。如果你不信的话，这是 $5 \times 5$ 时的路径：

代码见上。

---

以上为参考题解。例题2： 轻拍牛头 。

---

同余

其实这是提高组的内容。

同余的定义

字面意思。若两个整数 $a$ 和 $b$ 对 $m$ 的余数相同，则称 $a$ 和 $b$ 关于模 $m$ 同余，记作 $a \equiv b (\mod m)$ 。

不过也有人这样定义：若两个正整数 $a$ 和 $b$ ，它们的差 $a-b$ 能被某个自然数 $m$ 整除，则称 $a$ 和 $b$ 关于模 $m$ 同余，记作 $a \equiv b (\mod m)$ 。这其实也是同余的一个性质。

同余的性质

对于整数 $a, b, c$ 和自然数 $m, n$, 对模 $m$ 同余具有以下一些性质：

1. 自反性：$a \equiv a \pmod{m}$
2. 对称性：若 $a \equiv b \pmod{m}$, 则 $b \equiv a \pmod{m}$
3. 传递性：若 $a \equiv b \pmod{m}$, $b \equiv c \pmod{m}$, 则 $a \equiv c \pmod{m}$
4. 同加性：若 $a \equiv b \pmod{m}$, 则 $a + c \equiv b + c \pmod{m}$
5. 同乘性：若 $a \equiv b \pmod{m}$, 则 $a \times c \equiv b \times c \pmod{m}$

若 $a \equiv b \pmod{m}$, $c \equiv d \pmod{m}$, 则 $a \times c \equiv b \times d \pmod{m}$

6. 同幂性：若 $a \equiv b \pmod{m}$, 则 $a^n \equiv b^n \pmod{m}$
7. 推论 1: $a \times b \bmod k = (a \bmod k) \times (b \bmod k) \bmod k$
8. 推论 2: 若 $a \bmod p = x$, $a \bmod q = x$, $p, q$ 互质，则 $a \bmod (p \times q) = x$。

证明：因为 $a \bmod p = x$, $a \bmod q = x$, $p, q$ 互质

则一定存在整数 $s, t$, 使得 $a = s \times p + x$, $a = t \times q + x$

所以，$s \times p = t \times q$

则一定存在整数 $r$, 使 $s = r \times q$

所以，$a = r \times p \times q + x$, 得出：$a \bmod (p \times q) = x$

但是，同余不满足同除性，即不满足：$a \div n \equiv b \div n \pmod{m}$。

例题： 指数求余 、 H数 。（我也不知道和同余有什么关系）