前言

故意的。但是我没放代码。

---

选择题

选择题就随便蒙吧。

庆典队列

由题目也看得出来。最终答案：

$$n \div a$$

茶具套装组合

这应该是小学数学吧。

只需要在 $\frac{a}{1} 、 \frac{b}{1} 、 \frac{c}{1} 、 \frac{d}{4}$ 中取最小值。注意向下取整。最终答案：

$$\min(\frac{a}{1} , \frac{b}{1} , \frac{c}{1} , \frac{d}{4}) $$

平衡奇偶位置的字符交换

这应该是最奇妙的一道题了。

也许一看到题目时会想到 BFS ，但是搜索还是太麻烦了。想象一下有一串字符，其由 $\texttt{A}$ 和 $\texttt{B}$ 组成。在奇数位上有 $j$ 个 $\texttt{A}$ ，在偶数位上有 $o$ 个 $\texttt{A}$ 。你现在要使在奇偶数位上的 $\texttt{A}$ 相等，即要使 $j=o$ 。例如样例：

此时奇数位上的数字多了 $2$ ，那么就需要有 $2\div 2=1$ 个奇数位的 $\texttt{A}$ 需要移动到偶数位。所以答案就是 $\frac{j-o}{2}$ 。

这样也可以得到 $-1$ 的答案： 如果 $j-o$ 为奇数。因为是奇数时你可能就要移动 $0.5$ 个 $\texttt{A}$ 了。当然也需要注意 $j-o$ 为负数的情况。所以最终答案为：

$$\frac{|j-o|}{2}$$

矩阵圈层交错旋转

这是需要非常思维的模拟。可以分别模拟顺时针和逆时针旋转。我这里使用一个新的 b[][] 来存储答案。

例如这是顺时针：

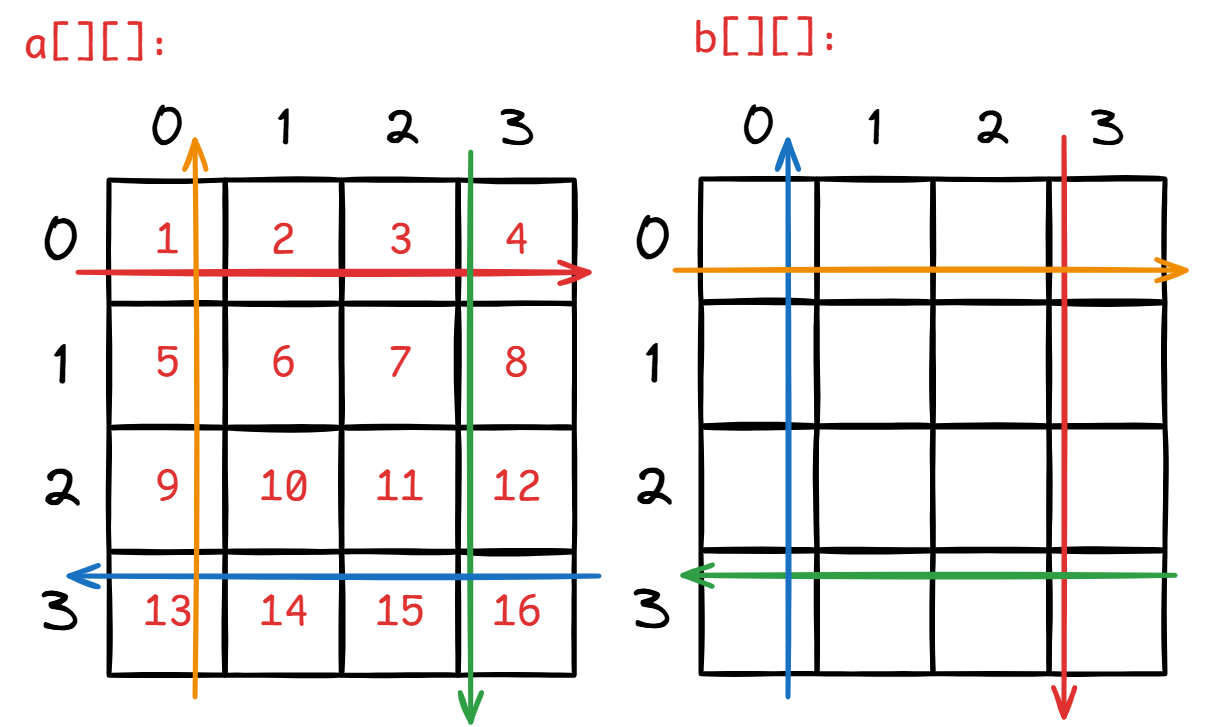
逆时针只需要反过来。然后注意一点细节。

环形取硬币游戏

剩下的有点 difficult 了。

鸣谢（洛谷用户）：Dark_Crown

1. $n$ 为奇数，此时 Jerry 只要把第一格全取完，转完一圈后 Tom 走到第一格就取不了了，所以 Jerry 必胜。

2. $n$ 为偶数，此时 Jerry 和 Tom 不会经过对方经过的格子 ，所以策略就是尽可能少取，把对面耗死。 称一个玩家硬币最少的格子中编号最小的为“X格”，那么假设 Jerry 的“X格”中的硬币数比 Tom 的“X格”多，那么 Jerry 必胜；反之，如果 Jerry 的“X格”中的硬币数比 Tom 的“X格”多，那么 Tom 必胜。如果双方“X格”中的硬币数一样多，那么谁的“X格”在更后面，谁就会赢。

魔术扑克牌排列

卡特兰数 + 高精度。