- gf24240 的博客
《梦溪笔谈·文化》卷十一:凹、凸透镜成像规律
- @ 2025-12-16 18:38:37
前言
其实不知道应该放文化还是科技。
透镜
透镜分为三种:
- 平面镜:光线进入后只会折射,平行光入射也会平行光折射。
- 凸透镜:中间厚,边缘薄。
- 凹透镜:中间薄,边缘厚。
凸透镜
例如,下面这是一个凸透镜:

凸透镜对光有会聚作用。
内容:
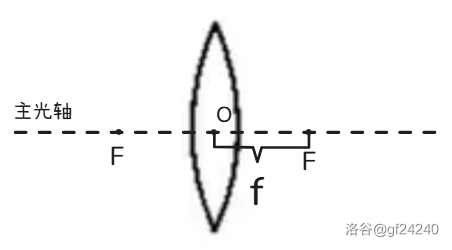
:光心(凸透镜中间)
:焦点(左右各一个)
:焦距(焦点到光心的距离,两段)
性质:
- 过心不变:当入射光线经过光心,经过凸透镜后任沿直线传播。
- 平行过焦:平行于主光轴入射的光线,折射光线会经过焦点。
- 过焦平行:入射光线(及其延长线)经过焦点,折射光线会平行于主光轴。
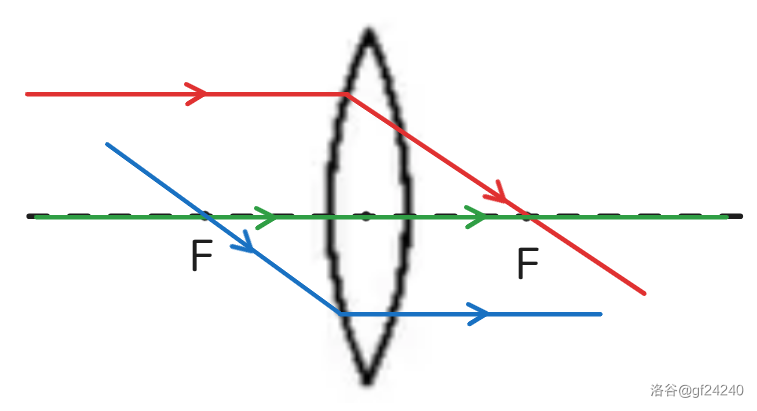
凹透镜
例如,下面这是一个凸透镜:

凹透镜对光有发散作用。
内容(类似凸透镜):
:光心(凹透镜中间)
:虚焦点(左右各一个)
:焦距(虚焦点到光心的距离,两段)
性质(类似凸透镜):
- 过心不变:当入射光线经过光心,经过凹透镜后任沿直线传播。
- 平行过焦:平行于主光轴入射的光线,其折射光的反向延长线线会经过(入射光线同侧的)虚焦点。
- 过焦平行:入射光线的延长线经过(另一侧的)虚焦点,折射光线会平行于主光轴。
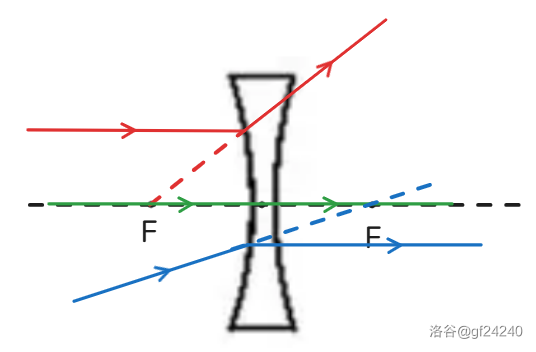
成像规律
根据上面“性质”中的特殊光线,我们可以通过画光路图探究凹、凸透镜的成像规律。
内容:
- :物距,即物体到凹/凸透镜的距离。
- :像距,即成像到凹/凸透镜的距离。
凸透镜
时
根据性质 和 ,得到以下光路图:
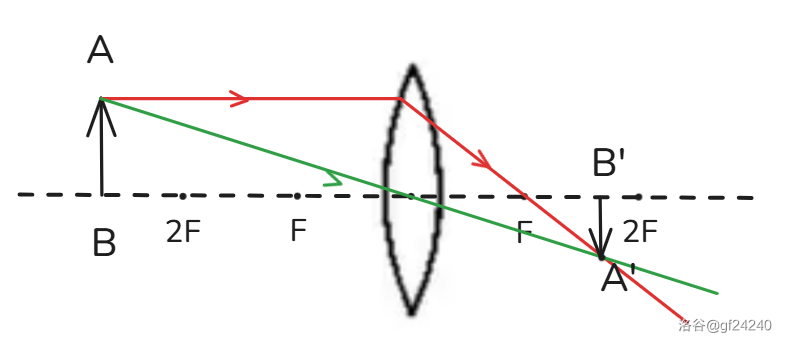
(注:绿色光线箭头有错位,不要在意)
得到结论:当 时,成倒立、缩小的实像,且 。
时
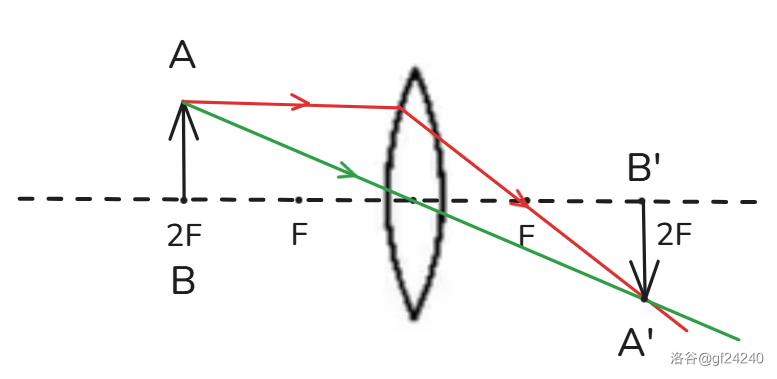
(注:图可能不太准确,但是理论上是这样的)
得到结论:当 时,成倒立、等大的实像,且 。
时
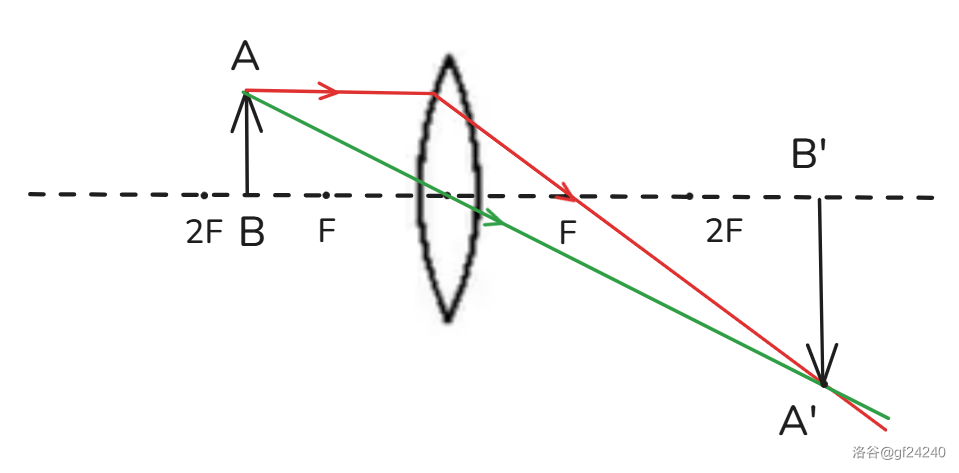
得到结论:当 时,成倒立、放大的实像,且 。
时
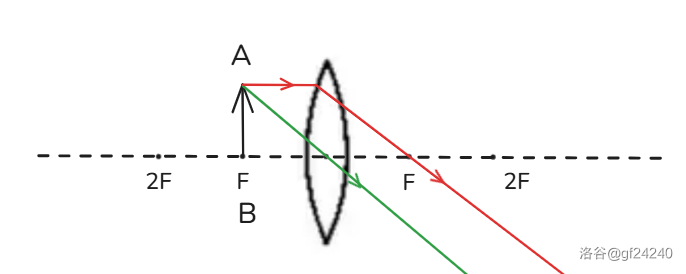
得到结论:当 时,不成像,没有 。
时
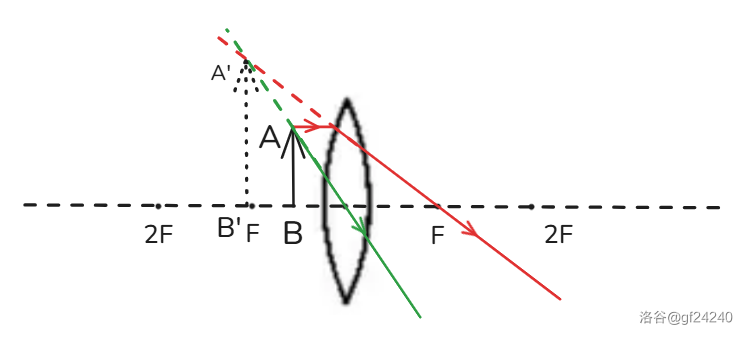
得到结论:当 时,成正立、放大的虚像,不确定。
总结
$$\textbf{凸透镜成像} \begin{cases} \textbf{倒立、缩小的实像} & u>2f \\ \textbf{倒立、等大的实像} & u=2f \\ \textbf{倒立、放大的实像} & f<u<2f \\ \textbf{不成像} & u=f \\ \textbf{正立、放大的虚像} & u<f \end{cases}$$凹透镜
时
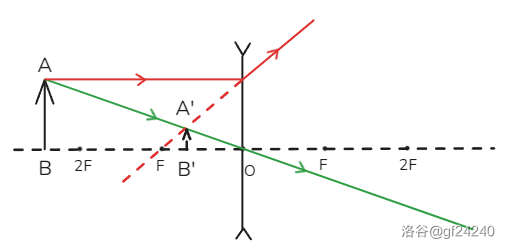
得到结论:当 时,成正立、缩小的虚像,不确定。
时
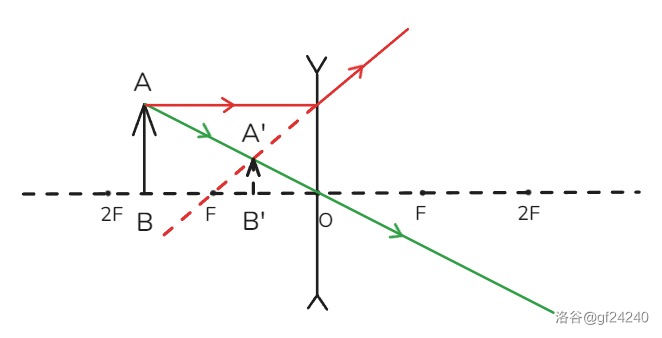
得到结论:当 时,成正立、缩小的虚像,不确定。
时
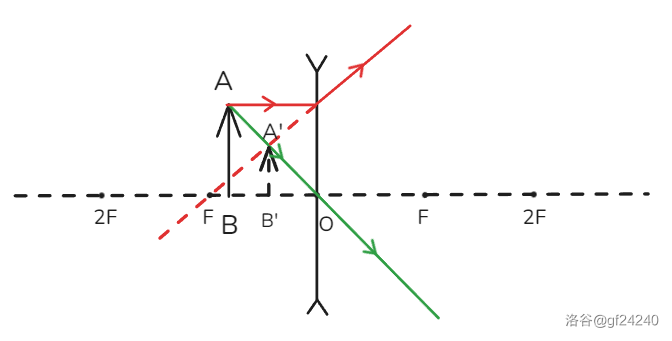
得到结论:当 时,成正立、缩小的虚像,不确定。
总结
凹透镜总是成正立、缩小的虚像。
