前言

洛谷还没有题目，。

---

题目我忘了。

T1

题目描述

有一个 $n$ 个节点的树，节点编号为 $1,2,3,...,n$。每一个节点初始的颜色都是白色。你每次操作可以使一个节点的颜色变为黑色。但是操作第 $i$ 个节点的代价是 $c_i$。你需要进行一些操作，使用最小的代价，使每一个叶子结点到根节点的路径中都有一个黑色的节点。求这个最小的代价。

输入格式

输入共三行。第一行：一个整数 $n$ 表示节点的数量。

第二行：$n-1$ 个整数 $f_2,f_3,f_4,...f_n$ 其中第 $i$ 个整数表示节点 $i$ 的父节点。保证 $f_i<i$。

第三行：$n$ 个整数 $c_1,c_2,c_3,...,c_n$ 表示操作节点 $i$ 的代价。

输出格式

输出共一行，一个整数表示代价。

T2

就是背包容量和物品体积有 $10^9$ 的 01 背包。

T1 题解

前言

其实在考场磨一小时多才有的代码。

一个奇怪的思路。利用动态规划的思想。

总体思路

定义 $dp_i$ 表示 $i$ 节点为根的子树的最小代价。

定义 $\text{son}(i)$ 表示节点 $i$ 的所有子节点。 容易发现 $dp_i=\min\left(c_i,\sum_{j\in\text{son}(i)}dp_j\right)$（即 $i$ 节点的所有子节点的最小操作代价的和）。

注意叶子结点的最小代价就是操作这个节点的最小代价。

最后答案就是 $dp_1$（因为根节点是 $1$）。

为什么可以这样做

如图。

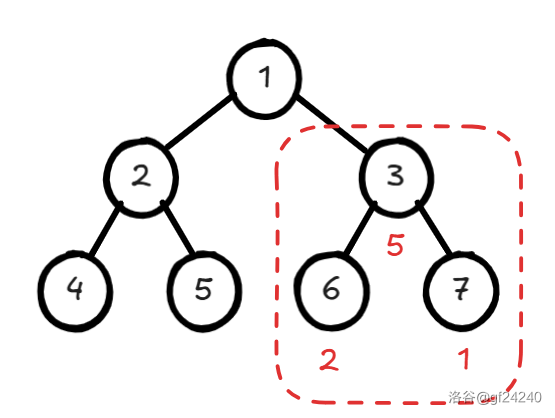
想要让 $6$ 和 $7$ 两个点符合有两种方法：

1. 操作节点 $6$ 和节点 $7$，代价 $2+1=3$，即 $i$ 的所有子节点的最小代价和。
2. 操作节点 $3$，代价 $5$，即 $c_i$。
3. （如果放在整张图中也可以操作节点 $1$，但是这里只有红色框中的树）

当然树的分支不止二叉。

例如计算图中红色框中的子树：

1. 计算叶子节点的最小代价：$dp_6=c_6=2,dp_7=c_7=1$。
2. 计算子节点更多的节点：$dp_3=\min\{c_3, dp_6+dp_7\}=\min\{5,3\}=3$。

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 1e5 + 5;
int n, f[N], cd[N], c[N], dp[N];
// n、f、c如题。cd[i]表示节点i以下的所有节点的数量 
// dp[i]表示以i为根的子树的最小代价。 
vector <int> crn[N], son[N];
// crn[i]表示节点i以下的所有节点
// son[i]表示i的子节点（直接与i相连） 

struct stu
{ // 子节点数和编号的结构体，用于 DP. 
	int cdNum, idx;
	bool operator <(const stu y)
	{ // 重定义比较运算，也可以写比较函数 
		return tie(cdNum, idx) < tie(y.cdNum, y.idx);
	}
}ndStu[N];

signed main()
{
	cin >> n;
	for (int i = 2; i <= n; ++i)cin >> f[i];
	for (int i = 1; i <= n; ++i)cin >> c[i];
	
	for (int i = n; i >= 2; --i)
	{ // 倒序，因为要求i一下所有节点的数量 
	  // 父节点要加上这个节点的所有子节点以下的所有节点和它子节点 
		cd[f[i]] += cd[i] + 1;
		crn[f[i]].push_back(i);
		for (auto u : crn[i])crn[f[i]].push_back(u);
	}

	for (int i = 1; i <= n; ++i)
	{ // 统计 
		ndStu[i] = {cd[i], i};
		son[f[i]].push_back(i);
	}
	// 按照子节点的数量从小到大排序（先处理叶子节点） 
	sort(ndStu + 1, ndStu + n + 1);

	for (int i = 1; i <= n; ++i)
	{
		int cNum = ndStu[i].cdNum, id = ndStu[i].idx; // 用变量替换方便处理 
		dp[id] = c[id]; // 叶子节点就是本身的代价，非叶子节点也要与本身的代价对比 
		if (cNum != 0)
		{ // 非叶子节点 
			int sum = 0; // 求所有子节点的最小代价和 
			for (auto u : son[id])sum += dp[u]; 
			dp[id] = min(dp[id], sum);
		}
	}
	// 根节点的最小代价 
	cout << dp[1];
	return 0; // 完结撒花 
}

补充

上面是是考场思路和代码（其实在考场写了一百多行）。当然有许多优化的地方：

1. 无需排序。题目保证 $f_i<i$，所以实际上可以直接从 $n$ 到 $1$ 进行 DP。
2. 不用存储 cd、crn、ndStu。实际上只需要 son 就够了（还有 dp 和题目的 f 和 c）。

所以以下是改进的代码，时间复杂度：$O(n)$。

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 1e5 + 5;
int n, f[N], c[N], dp[N];
// n、f、c如题。dp[i]表示以i为根的子树的最小代价。 
vector <int> son[N];

signed main()
{
	cin >> n;
	for (int i = 2; i <= n; ++i)
	{
		cin >> f[i];
		son[f[i]].push_back(i);
	}
	for (int i = 1; i <= n; ++i)cin >> c[i];

	for (int i = n; i >= 1; --i)
	{
		dp[i] = c[i]; // 叶子节点就是本身的代价，非叶子节点也要与本身的代价对比 
		if (!son[i].empty())
		{ // 非叶子节点 
			int sum = 0; // 求所有子节点的最小代价和 
			for (auto u : son[i])sum += dp[u]; 
			dp[i] = min(dp[i], sum);
		}
	}
	// 根节点的最小代价 
	cout << dp[1];
	return 0; // 完结撒花 
}

总体思路和之前差不多，但是时间和空间都有很大优化。