- gf24118 的博客
GF2025C2数论1
- @ 2025-8-1 16:48:38
数论!!!
放课件在下面了
先是数论中的整除
整除概念如下:
设是非零整数,是整数。如果存在一个整数,使得,那么就说可被整除,记作,且称是的倍数,是的约数(因子)。
这是整除性质:
1.如果且,那么。
2.且等价于对任意的整数和,有。
3.设,那么等价于。
4.设整数和满足下式:,且、,那么。
补充证明过程:
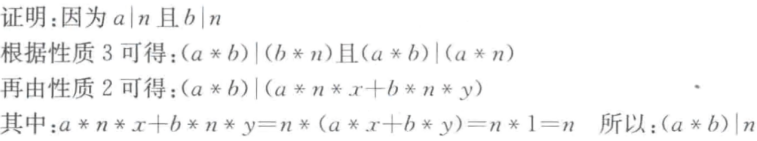
5.若,那么的充分条件是。
整除补充:

以下是整数性质:
- 任何一个正整数,都可以写成的形式,其中为非负整数,l为奇数。
- 若,,则的除以外的最小正因数q是一个质(素)数,如果,则。
- 推论:如果不超过的所有质数均不是的约数,则必为质数。
补充性质2

余数三大定理
- 1.余数的加法定理。
与的和除以的余数,等于、分别除以的余数之和,或这个和除以的余数。当余数的和比除数大时,所求的余数等于余数之和再除以的余数。
- 2.余数的减法定理。
与的差除以的余数,等于、分别除以的余数之差。当余数的差不够减时,补上除数再减。
- 3.余数的减法定理。
与的乘积除以的余数,等于、分别除以的余数的积,或者这个积除以所得的余数。当余数的积比除数大时,所求的余数等于余数之积再除以的余数。
