gf24118 的博客
GF2025C2卡特兰数&离散数学(概率与期望)
gf24118 LV 8 @ 2025-8-12 11:09:48

卡特兰数&离散数学(概率与期望)！！！

前言

666打这篇博客给编者打成傻子了，有点乱将就着看吧(编者已经很努力让本博客变整洁了QwQ)，太多了还得出后续(其实真不用)

卡特兰数

应用

卡特兰数可以应用至以下场景: 有 $2n$ 只person排成一行进入哥哥的演唱会。入场费 5 元。其中只有 $n$ 只person有一张 $5$ 元钞票，另外 $n$ 只person只有 $10$ 元钞票，剧院无其它钞票，问有多少种方法使得只要有 10 元的person买票，售票处就有 5 元的钞票找零？

哥哥演唱会be like:(点击查看)

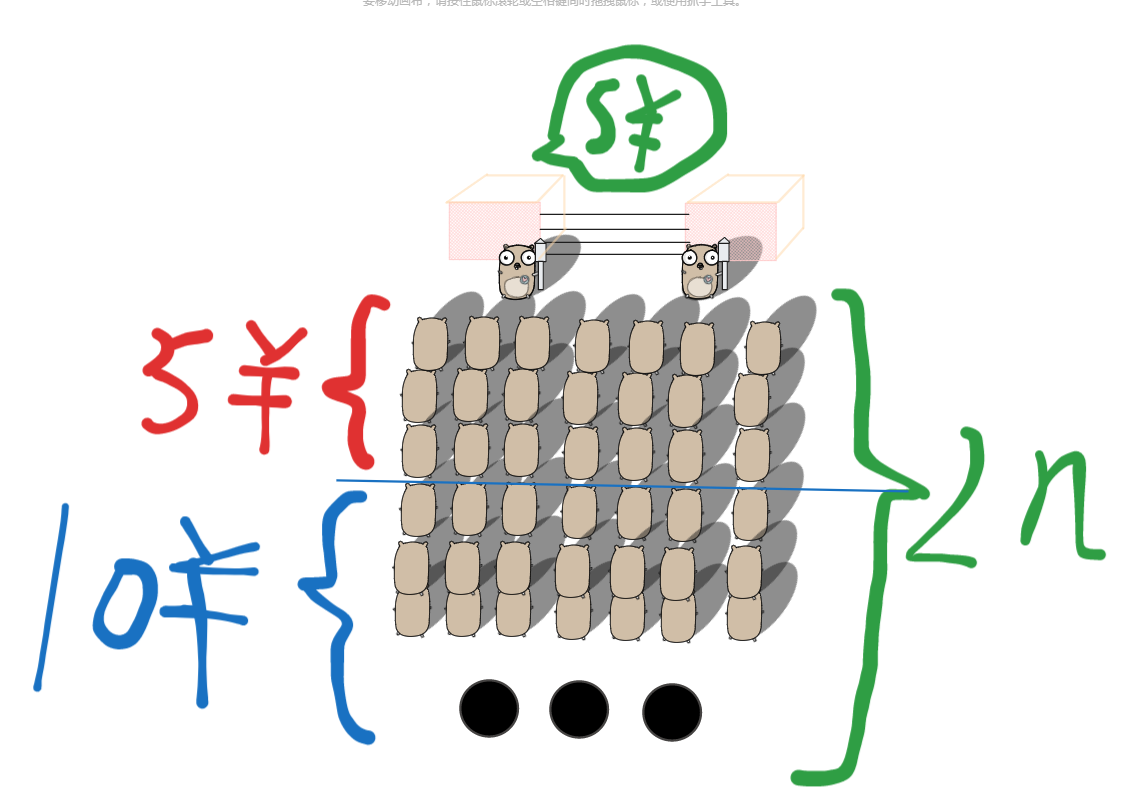
关系式以及代码

编者注:依旧枯燥

递推关系

该递推关系的解为：

$$H_n = \frac{\binom{2n}{n}}{n+1}(n \geq 2, n \in \mathbf{N_{+}}) $$

关于卡特兰数数的常见公式：

$$H_n = \begin{cases} \sum_{i=1}^{n} H_{i-1} H_{n-i} & n \geq 2, n \in \mathbf{N_{+}}\\ 1 & n = 0, 1 \end{cases}$$

H_n = \frac{H_{n-1} (4n-2)}{n+1}

H_n = \binom{2n}{n} - \binom{2n}{n-1}

此方式c++代码:

#include <iostream>
using namespace std;
int n;
long long f[25];

int main() {
  f[0] = 1;
  cin >> n;
  for (int i = 1; i <= n; i++) f[i] = f[i - 1] * (4 * i - 2) / (i + 1);
  // 这里用的是常见公式2
  cout << f[n] << endl;
  return 0;
}

封闭形式

编者注:看不懂别硬看，跳过或者直接记结论就行。

卡特兰数的递推式为

H_n=\sum_{i=0}^{n-1}H_{i}H_{n-i-1} \quad (n\ge 2)

其中 $H_0=1,H_1=1$ 。设它的普通生成函数为 $H(x)$ 。

我们发现卡特兰数的递推式与卷积的形式很相似，因此我们用卷积来构造关于 $H(x)$ 的方程：

$$\begin{aligned} H(x)&=\sum_{n\ge 0}H_nx^n\\ &=1+\sum_{n\ge 1}\sum_{i=0}^{n-1}H_ix^iH_{n-i-1}x^{n-i-1}x\\ &=1+x\sum_{i\ge 0}H_{i}x^i\sum_{n\ge 0}H_{n}x^{n}\\ &=1+xH^2(x) \end{aligned}$$

解得

H(x)=\frac{1\pm \sqrt{1-4x}}{2x}

那么这就产生了一个问题：我们应该取哪一个根呢？我们将其分子有理化：

H(x)=\frac{2}{1\mp \sqrt{1-4x}}

代入 $x=0$ ，我们得到的是 $H(x)$ 的常数项，也就是 $H_0$ 。当 $H(x)=\dfrac{2}{1+\sqrt{1-4x}}$ 的时候有 $H(0)=1$ ，满足要求。而另一个解会出现分母为 $0$ 的情况（不收敛），舍弃。

因此我们得到了卡特兰数生成函数的封闭形式：

H(x)=\frac{1- \sqrt{1-4x}}{2x}

接下来我们要将其展开。但注意到它的分母不是斐波那契数列那样的多项式形式，因此不方便套用等比数列的展开形式。在这里我们需要使用牛顿二项式定理。我们来先展开 $\sqrt{1-4x}$ ：

$$\begin{aligned} (1-4x)^{\frac{1}{2}} &=\sum_{n\ge 0}\binom{\frac{1}{2}}{n}(-4x)^n\\ &=1+\sum_{n\ge 1}\frac{\left(\frac{1}{2}\right)^{\underline{n}}}{n!}(-4x)^n \end{aligned} \tag{1}$$

注意到

$$\begin{aligned} \left(\frac{1}{2}\right)^{\underline{n}} &=\frac{1}{2}\frac{-1}{2}\frac{-3}{2}\cdots\frac{-(2n-3)}{2}\\ &=\frac{(-1)^{n-1}(2n-3)!!}{2^n}\\ &=\frac{(-1)^{n-1}(2n-2)!}{2^n(2n-2)!!}\\ &=\frac{(-1)^{n-1}(2n-2)!}{2^{2n-1}(n-1)!} \end{aligned}$$

这里使用了双阶乘的化简技巧。那么带回 $(1)$ 得到

$$\begin{aligned} (1-4x)^{\frac{1}{2}} &=1+\sum_{n\ge 1}\frac{(-1)^{n-1}(2n-2)!}{2^{2n-1}(n-1)!n!}(-4x)^n\\ &=1-\sum_{n\ge 1}\frac{(2n-2)!}{(n-1)!n!}2x^n\\ &=1-\sum_{n\ge 1}\binom{2n-1}{n}\frac{1}{(2n-1)}2x^n \end{aligned}$$

带回原式得到

$$\begin{aligned} H(x)&=\frac{1- \sqrt{1-4x}}{2x}\\ &=\frac{1}{2x}\sum_{n\ge 1}\binom{2n-1}{n}\frac{1}{(2n-1)}2x^n\\ &=\sum_{n\ge 1}\binom{2n-1}{n}\frac{1}{(2n-1)}x^{n-1}\\ &=\sum_{n\ge 0}\binom{2n+1}{n+1}\frac{1}{(2n+1)}x^{n}\\ &=\sum_{n\ge 0}\binom{2n}{n}\frac{1}{n+1}x^{n}\\ \end{aligned}$$

这样我们就得到了卡特兰数的通项公式。

好，我们再看一下编者搜索的卡特兰数代码。

#include <bits/stdc++.h>
using namespace std;
int  ktls(int n){
	if(n<=1) return 1;
	int *h=new int [n+1];
	h[0]=h[1]=1;
	for(int i=2;i<=n;i++){
		h[i]=0;
		for(int j=0;j<i;j++) h[i]+=(h[j]*h[i-1-j]);
	}
	int result=h[n];
	delete [] h;
	return result;
}
int main() {
	int n;
	cin>>n;
	cout<<ktls(n);
	return 0;
}

离散数学(概率与期望)

基本概念概述

在研究具体的随机现象时我们通常着重关注以下要素：

样本空间: $\Omega$ ，指明随机现象所有可能出现的结果。
事件域: $\mathcal{F}$ ，表示我们所关心的所有事件。
概率: $P$ ，描述每一个事件发生的可能性大小。

样本空间、随机事件

定义

一个随机现象中可能发生的不能再细分的结果被称为样本点。所有样本点的集合称为样本空间，通常用 $\Omega$ 来表示。

一个随机事件是样本空间 $\Omega$ 的子集，它由若干样本点构成，用大写字母 $A$ , $B$ , $C$ , \cdots 表示。好，对于一个随机现象的结果 $\omega$ 和一个随机事件 $A$ ，我们称事件 $A$ 发生了当且仅当 $\omega \in A$ 。

好了咱们举个栗子生动说明，爱吃土豆、马铃薯和potato是一个随机现象，其样本空间可以表示为 $\Omega=\{1,2,3\}$ 。设随机事件 $A$ 为「获得的点数大于 $2$ 」，则 $A = \{ 3 \}$ 。若某次发现爱吃土豆等东西 $\omega = 1$ ，由于 $\omega \notin A$ ，故事件 $A$ 没有发生。

事件的运算

由于我们将随机事件定义为了样本空间 $\Omega$ 的子集，故我们可以将集合的运算（如交、并、补等）移植到随机事件上。记号与集合运算保持一致。

还有一些比较特别，事件的并 $A \cup B$ 也可记作 $A + B$ ，事件的交 $A \cap B$ 也可记作 $AB$ ，此时也可分别称作 $和事件$ 和 $积事件$ 。

概率

概率概述

概率的公理化定义：

概率函数 $P$ 是一个从事件域 $\mathcal{F}$ 到闭区间 $[0, 1]$ 的映射，且满足：

规范性：事件 $\Omega$ 的概率值为 $1$ ，即 $P(\Omega)=1$ 。
可数可加性：若一列事件 $A_1$ , $A_2$ , $\cdots$ 两两不交，则 $P\left( \bigcup_{i \geq 1} A_i \right) = \sum_{i \geq 1} P(A_i)$。

概率函数的性质

对于任意随机事件(比如明天开学、天降马铃薯) $A$ , $B \in \mathcal{F}$ ，有:

单调性：若 $A \subset B$ ，则有 $P(A) \leq P(B)$ 。
容斥原理： $P(A+B) = P(A) + P(B) - P(AB)$ 。 $P(A - B) = P(A) - P(AB)$ ，这里 $A - B$ 表示差集。

我们在一开始提到，研究具体的随机现象时我们通常关注样本空间 $\Omega$ 、事件域 $\mathcal{F}$ 以及概率函数 $P$ 。我们将三元组 $(\Omega, \mathcal{F}, P)$ 称为一个概率空间。

条件概率

定义

若已知事件 $A$ 发生，在此条件下事件 $B$ 发生的概率称为条件概率，记作 $P(B|A)$ 。

在概率空间 $(\Omega, \mathcal{F}, P)$ 中，若事件 $A \in \mathcal{F}$ 满足 $P(A) > 0$ ，则条件概率 $P(\cdot|A)$ 定义为

$$P(B|A) = \frac{P(AB)}{P(A)} \quad \forall B \in \mathcal{F} $$

可以验证根据上式定义出的 $P(\cdot|A)$ 是 $(\Omega, \mathcal{F})$ 上的概率函数。

根据条件概率的定义可以直接推出下面两个等式：

概率乘法公式：在概率空间 $(\Omega, \mathcal{F}, P)$ 中，若 $P(A) > 0$ ，则对任意事件 $B$ 都有

P(AB) = P(A)P(B|A)

全概率公式：在概率空间 $(\Omega, \mathcal{F}, P)$ 中，若一组事件 $A_1$ , $\cdots, A_n$ 两两不交且和为 $\Omega$ ，则对任意事件 $B$ 都有

P(B) = \sum_{i=1}^{n} P(A_i)P(B|A_i)

事件

事件的独立性

在研究条件概率的过程中，可能会出现 $AP(B|A) = P(B)$ 的情况。从直观上讲就是事件 $B$ 是否发生并不会告诉我们关于事件 $A$ 的任何信息，即事件 $B$ 与事件 $A$ 「无关」。于是我们就有了下面的定义

定义

若同一概率空间中的事件 $A$ , $B$ 满足 $P(AB) = P(A)P(B)$ 则称 $A$ , $B$ 独立。对于多个事件 $A_1$ , $A_2$ , $\cdots, A_n$ ，我们称其独立，当且仅当对任意一组事件 $\{ A_{i_k} : 1 \leq i_1 < i_2 < \cdots < i_k \leq n \}$ 都有

$$P( A_{i_1}A_{i_2} \cdots A_{i_r} ) = \prod_{k=1}^{r} P(A_{i_k}) $$

多个事件的独立性

对于多个事件，一般不能从两两独立推出这些事件独立。考虑以下反例：有一个正四面体骰子，其中三面被分别涂成红色、绿色、蓝色，另一面则三色皆有。现在扔一次该骰子，令事件 $A$ , $B$ , $C$ 分别表示与桌面接触的一面包含红色、绿色、蓝色。

不难计算 $P(A) = P(B) = P(C) = \frac{1}{2}$ ，而 $P(AB) = P(BC) = P(CA) = P(ABC) = \frac{1}{4}$ 。

显然 $A$ , $B$ , $C$ 两两独立，但由于 $P(ABC) \neq P(A)P(B)P(C)$ ，故 $A$ , $B$ , $C$ 不独立。

GF2025C2卡特兰数&离散数学(概率与期望)

卡特兰数&离散数学(概率与期望)！！！

前言

卡特兰数

应用

关系式以及代码

递推关系

此方式c++代码:

封闭形式

好，我们再看一下编者搜索的卡特兰数代码。

离散数学(概率与期望)

基本概念概述

样本空间、随机事件

定义

事件的运算

概率

概率概述

概率的公理化定义：

概率函数的性质

条件概率

定义

根据条件概率的定义可以直接推出下面两个等式：

事件

事件的独立性

定义

多个事件的独立性

状态

开发

支持

GF2025C2卡特兰数&离散数学(概率与期望)

卡特兰数&离散数学(概率与期望)！！！

前言

卡特兰数

应用

关系式以及代码

递推关系

此方式c++代码:

封闭形式

好，我们再看一下编者搜索的卡特兰数代码。

离散数学(概率与期望)

基本概念概述

样本空间、随机事件

定义

事件的运算

概率

概率概述

概率的公理化定义：

概率函数的性质

条件概率

定义

根据条件概率的定义可以直接推出下面两个等式：

事件

事件的独立性

定义

多个事件的独立性

状态

开发

支持

还没有账户？

登录