- gf25003 的博客
容斥原理
- @ 2025-8-9 20:22:13
容斥原理
集合的容斥关系
由于markdown不会打,所以我直接用截图吧。。。 举个例子,班上有的人学信奥,有的人学画画,但有人既学信奥又学画画,这就是容斥原理。
(三)容斥原理
公式太复杂了,记文字吧
所有集合-两个集合的∩+三个集合的交-四个集合的∩ ......
举个例子,班上有的人学信奥,有的人学画画,但有人既学信奥又学画画,这就是容斥原理。
(三)容斥原理
公式太复杂了,记文字吧
所有集合-两个集合的∩+三个集合的交-四个集合的∩ ......
来看点例题 例一:有多少个能被3或5或7整除的小于1000的正整数?
分析:设,,分别表示被3整除,被5整除,被7整除的数构成的集合,根据公式:
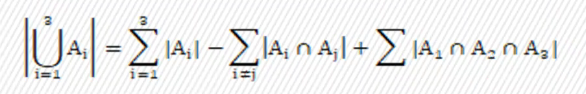 (还是不会打,依旧用截图)
(还是不会打,依旧用截图)
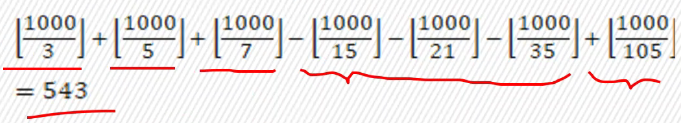
错位排列
(一)错位排列的定义
对于一个1......n的任意排列,有一种情况是地i格位置上的数不是i对任意i都成立,例如n=3是,有且仅有231和312是满足要求的,这样的排列被称为错位排列。
现在的问题是:能否对于任意n,给出错位排列二的个数?
分析:利用容斥原理
由容斥原理,我们可以得到错位排列公式:
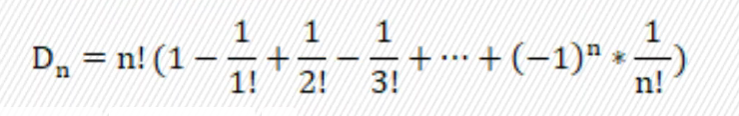 也约等于,e=2.71828
(二)错位排列的递推关系
(懒得写了)
也约等于,e=2.71828
(二)错位排列的递推关系
(懒得写了)

期望与概率
(一)等可能时间的概率,如果一次实验共有n中等可能出现的结构,其中事件A包含的结果有m中,那么事件A的概率为
(二)概率计算中的几个常用公式

