二分法的前提是：有序序列或者答案值区间是有序的

二分查找的写法按照区间设置的不同有三种写法，它们最大的不同点是每次缩小范围的时候L或R的赋值不同，以及最后答案所在位置不同。

一、1型，区间为一闭一开(L,R]或[L,R)：

代码标志行：while(R-L>1)

（1）【1型】最大值最小类型的前开后闭区间写法：

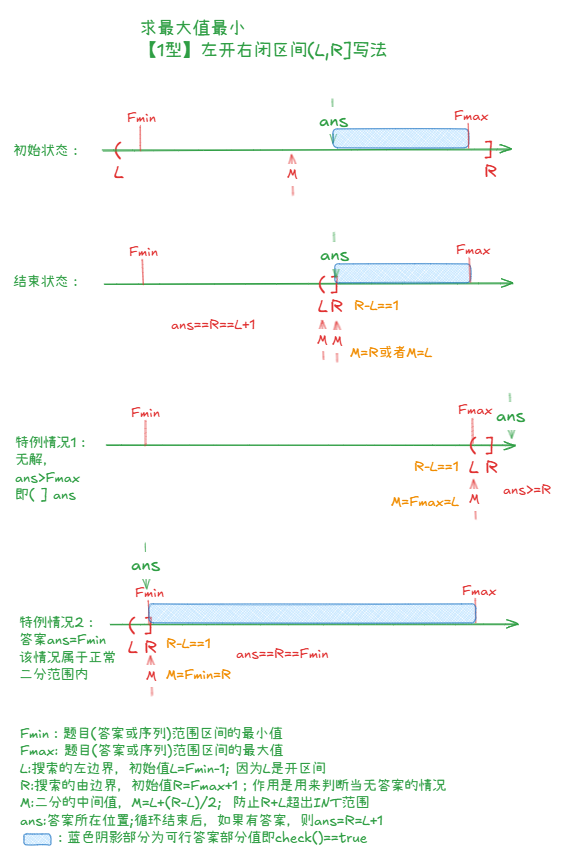
//求最大值最小，前开后闭区间(L,R]
	int L,R,M;
	L=amin-1,R=amax+1;//答案区间范围(L,R],L是答案的下限-1，R是答案的上限+1；
	//注意区间范围宁可过大，也不要过小
	//L是开区间所以需要-1，R虽然是闭区间但是为了验证找不到答案的情况范围也需要扩大1
	while(R-L>1){//只要(L,R]区间超过1个数，继续二分查找 
		M=L+(R-L)/2;//二分，等价于=(r+l)/2，这样写防止r+l爆int范围 
		if(check(M)){//如果M是可行的答案 
			//ans=M;//可不写 
			R=M;//缩小R,由于(L,R],R表示可能是答案，所以这里不需要M-1 
		}else{//否则M不是答案 
			L=M;//缩小L，由于(L,R],L本身不是答案，所以不需要M+1; 
		}
	}
	if(R!=amax+1)//最后只要R有移动过，那么找到答案 
		cout<<R;//最后停止在区间(L,R]即(ans-1,ans]; 
	else//如果R未移动过，就是答案不在(L,R]范围内 
		cout<<"No answer";//最后停止在区间(amax,amax+1]; 
	//这种写法答案可以为：L+1==R==ans
	

（2）【1型】最小值最大类型的前闭后开区间写法：

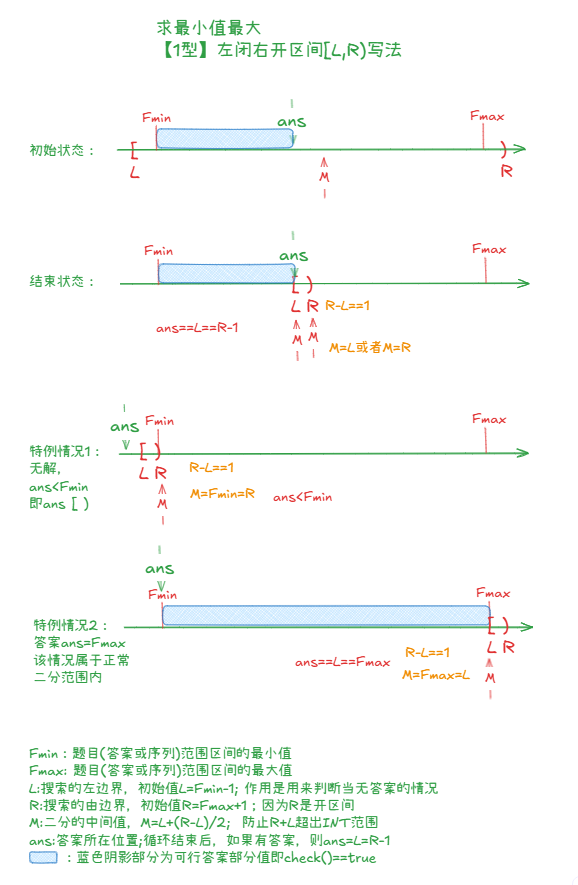
	//求最小值最大，前闭后开区间[L,R) 
	int L,R,M;
	L=amin-1,R=amax+1;
	while(R-L>1){//[)
		M=L+(R-L)/2;
		if(check(M)){
			//ans=M;//可不写 
			L=M;
		}else{
			R=M;
		}
	}
	if(L!=amin-1)
		cout<<L;//[L,R)即[ans,ans+1)
	else
		cout<<"No answer";
	//这种写法答案可以为：L==R-1==ans

2、0型，区间为闭合区间[L,R]

代码标志行：while(L<R) //while(R-L>0)

（1）【0型】最大值最小类型的前闭后闭区间写法：

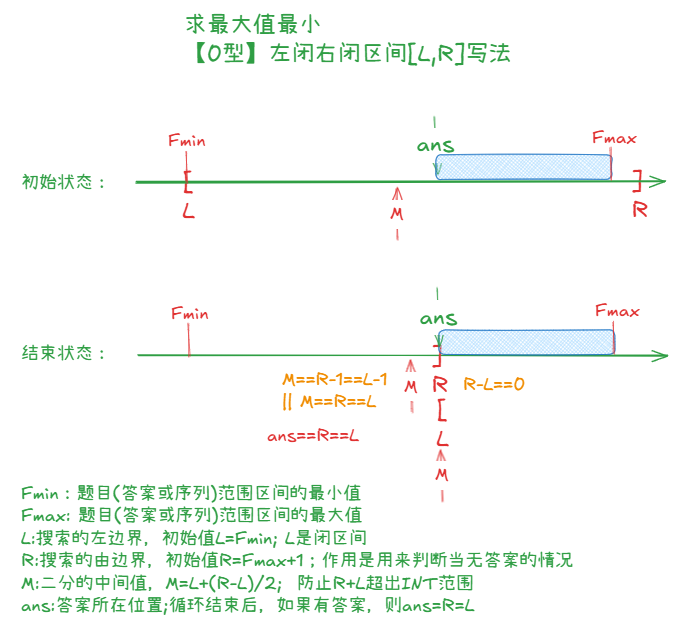
//求最大值最小，前闭后闭区间[L,R]
	int L,R,M,ans;
	L=amin,R=amax+1;
	while(L<R){//[],即 R-L>0
		M=L+(R-L)/2;
		if(check(M)){
			ans=m;//可不写 
			R=M;
		}else{
			L=M+1;
		}
	}
	if(R!=amax+1)
		cout<<R;//[L,R],L==R==ans
	else
		cout<<"No answer";	
	//这种写法答案可以为：L==R==ans

（2）【0型】最小值最大类型的前闭后闭区间写法：

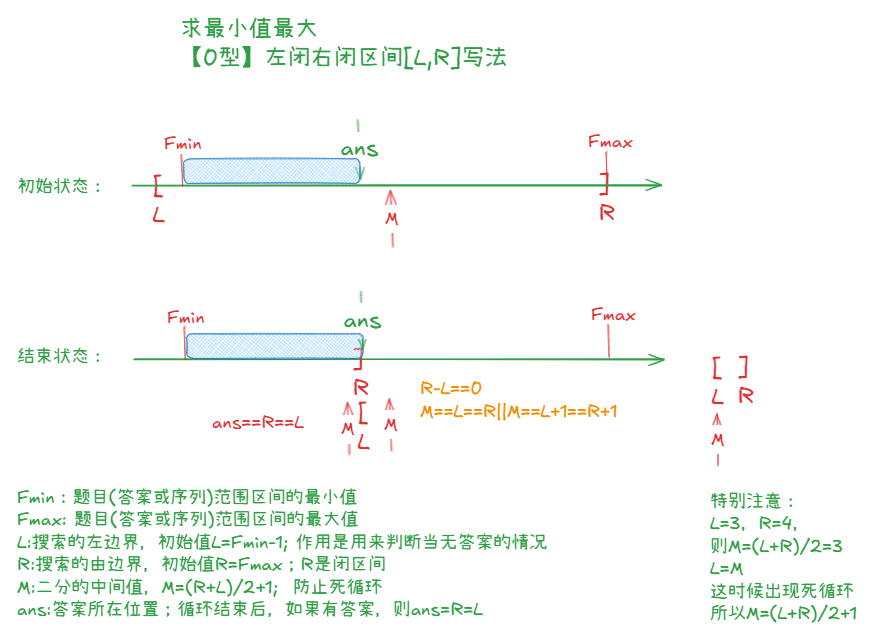
	//求最小值最大，前闭后闭区间[L,R] 
	int L,R,M,ans;
	L=amin-1,R=amax;
	while(L<R){//[],即 R-L>0
		M=L+(R-L)/2+1;//注意这里M=(L+R)/2+1; 否则while死循环
		if(check(M)){
			ans=m;//可不写 
			L=M;
		}else{
			R=M-1;
		}
	}
	if(L!=amin-1)
		cout<<L;//[L,R],L==R==ans
	else
		cout<<"No answer";
	//这种写法答案可以为：L==R==ans

3、-1型，区间为闭合区间[L,R]

代码标志行：while(L<=R) //while(R-L>-1)

（1）【-1型】最大值最小类型的前闭后闭区间写法：

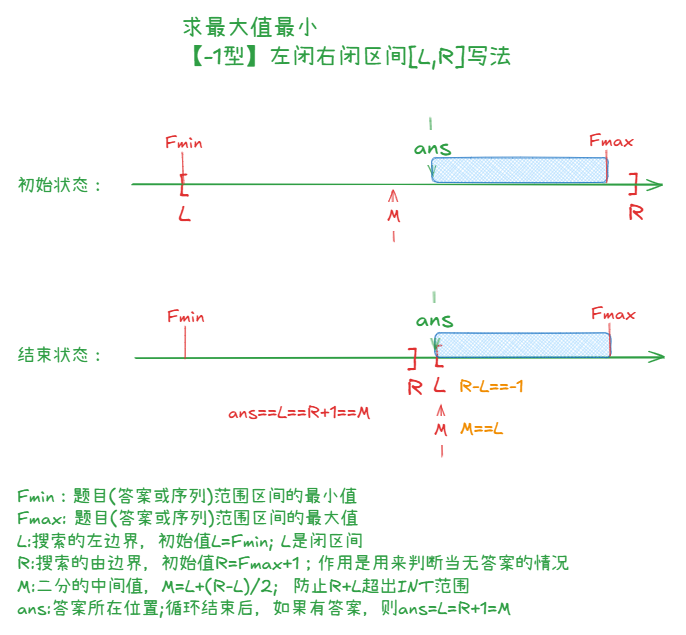
	//求最大值最小，前闭后闭区间[L,R]
	int L,R,M,ans;
	L=amin,R=amax+1;
	while(L<=R){//][,即 R-L>-1 或 R-L>=0 
		M=L+(R-L)/2;
		if(check(M)){
			ans=m;//可不写,但是一般会用ans定位答案 
			R=M-1;
		}else{
			L=M+1;
		}
	}
	if(R!=amax+1)
		cout<<ans;//[R,L],L和R错位 ],[ 。
	else
		cout<<"No answer";		
	//这种写法答案可以为：ans==L==R+1

（2）【-1型】最小值最大类型的前闭后闭区间写法：

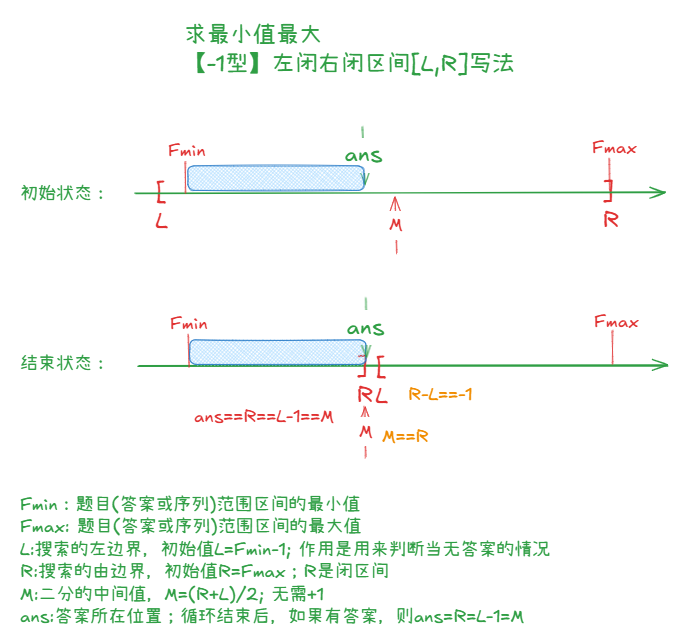
	//求最小值最大，前闭后闭区间[L,R] 
	int L,R,M,ans;
	L=amin-1,R=amax;
	while(L<=R){//][,即 R-L>-1 或 R-L>=0 
		M=L+(R-L)/2;//注意这里M不需要+1，因为L=M+1不会造成while死循环
		if(check(M)){
			ans=m;//可不写,但是一般会用ans定位答案
			L=M+1;
		}else{
			R=M-1;
		}
	}
	if(L!=amin-1)
		cout<<ans;//[R,L],L和R错位 ],[ 
	else
		cout<<"No answer";
	//这种写法答案可以为：ans==R==L-1

以上三种写法“1型”代码最简单，所以推荐使用“1型”，但是大部分初赛题目，都会出代码较复杂的“0型”和“-1型”，所以上述三种写法都要掌握。

只要掌握了老师讲的坐标轴区间画法，那么三种写法都能轻松搞定。

另外关于区间L,R的初始值设定宁可超过，不可不够

如果无法分析范围区间的时候，可以直接设置为题目给的数据范围的最大范围区间即可