#D1001. GCD和LCM是好朋友(数据轻松版)
GCD和LCM是好朋友(数据轻松版)
背景
1. 最大公约数
1.1 基本概念
最大公因数,也称最大公约数、最大公因子,指两个或多个整数共有约数中最大的一个。a,b的最大公约数记为,同样的,的最大公约数记为,多个整数的最大公约数也有同样的记号。求最大公约数有多种方法,常见的有质因数分解法、短除法、辗转相除法、更相减损法。与最大公约数相对应的概念是最小公倍数,的最小公倍数记为[]。
1.2 算法
短除法
求的最大公约数:
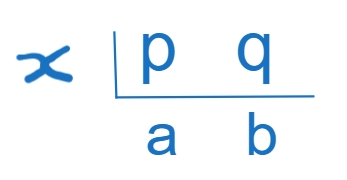
当为互质数时候,为最大公约数,为最小公倍数
辗转相除法
辗转相除法:辗转相除法是求两个自然数的最大公约数的一种方法,也叫欧几里德算法。
用辗转相除法求几个数的最大公约数,可以先求出其中任意两个数的最大公约数,再求这个最大公约数与第三个数的最大公约数,依次求下去,直到最后一个数为止。最后所得的那个最大公约数,就是所有这些数的最大公约数。

2. 最小公倍数
2.1 基本概念
两个或多个整数公有的倍数叫做它们的公倍数,其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数。整数a,b的最小公倍数记为[],同样的,的最小公倍数记为[],多个整数的最小公倍数也有同样的记号。
与最小公倍数相对应的概念是最大公约数,a,b的最大公约数记为()。关于最小公倍数与最大公约数,我们有这样的定理:()[]=(均为整数)
2.2 算法
公式法
由于两个数的乘积等于这两个数的最大公约数与最小公倍数的积。即。所以,求两个数的最小公倍数,就可以先求出它们的最大公约数,然后用上述公式求出它们的最小公倍数。
题目说明
已知两个正整数 P,Q的GCD(P,Q)是x,LCM(P,Q)是y,求出满足上述条件的P,Q的对数有几对。
输入格式
每个测试文件只包含一组测试数据,每组两个正整数x和y。
输出格式
对于每组输入数据,输出满足条件的所有可能的两个正整数的对数的方案总数。
样例
3 604下面是对样例数据的说明:
输入3 60
此时的分别为:
| 序号 | ||
|---|---|---|
所以上述有4种可能,输出答案4
数据范围
| 测试点 | x范围 | y范围 |
|---|---|---|
| ~ |
