背景：鉴于D老师自从2024年12月14日就开始讲DFS，一直到2025年4月26（可能更久）还在讲BFS，著此文章致敬D老师（此文章并不能作为教材，充其量是复习资料）

---

深度优先搜索（DFS/大法师）

目录：

1. 连通块问题-洪水填充(Flood fill)算法
2. 地图路径问题
3. 地图最小步数问题
4. 排列组合问题
5. 综合DFS
6. DFS简单优化和剪枝

---

1.连通块问题

连通块，顾名思义就是连在一起的块。先上道题：红与黑。题目意思：求从@开始最大的.的连通块，四方向。

（按D老师的思路）先尝试用递归来解决本题：定义即可用，先定义一个数步数的函数step(int x, int y)。从@开始，每次向上、下、左、右递归调用step，代码如下：

#include <iostream>
using namespace std;
int n, m, ans, sx, sy;
char a[10005][10005];
void step(int x, int y)
{
  if (x < 1 || x > n)return ;
  if (y < 1 || y > m)return ;
  if (a[x][y] == '#')return ;
  
  a[x][y] = '#';
  ans++;
  
  step(x + 1, y);
  step(x - 1, y);
  step(x, y + 1);
  step(x, y - 1);
}
int main()
{
  cin >> m >> n;
  for (int i = 1; i <= n; i++)
  {
  	for (int j = 1; j <= m; j++)
  	{
  		cin >> a[i][j];
  		if (a[i][j] == '@')
  		{
  			a[i][j] = '.';
  			sx = i, sy = j;
  		}
  	}
  }
  step(sx, sy);
  cout << ans;
  return 0;
}

如果我们把形式稍微改变，并将step改为dfs，就能得到深搜的代码：

int dx[] = {0, 1, -1, 0, 0};
int dy[] = {0, 0, 0, 1, -1};
void dfs(int x, int y)
{
	if (a[x][y] == '#')return ;
	if (x < 1 || y < 1 || x > n || y > m)return ;
	a[x][y] = '#';
	ans++;

	for (int i = 1; i <= 4; i++)
	{
		int nx = x + dx[i];
		int ny = y + dy[i];
		dfs(nx, ny);
	}
}

四方向的题目用dx[]和dy[]不是很方便，如果是八方向（数池塘）或十二方向（人造星空）呢。。。

---

2.地图路径问题 && 3.地图最小步数问题

迷宫游戏都玩过吧？

深搜也可以用来搜索迷宫路径！（其实和连通块是一个道理，起点和终点只要连通就是一条路径）在多定义一个way[]，用来存储路径。再加上if()判断是否到达终点。再稍微改变形式，你就得到了搜索迷宫路径的代码（迷宫的路径）：

bool check(int x,int y)
{
    if (a[x][y] == 0)return 0;
    return 1;
}
void dfs(int x,int y)
{
    if (x == n && y == m)
    {
        flag = "";
        rnum++;
        print();
        return;
    }

    //cout << "\n*\n";//
    for (int i = 1; i <= 4; i++)
    {
        int nx = x + dx[i];
        int ny = y + dy[i];
        if (check(nx,ny))
        {
            wi++;
            a[nx][ny] = 0;
            way[wi] = {nx,ny};
            dfs(nx,ny);
            way[wi] = {0,0};
            a[nx][ny] = 1;
            wi--;
        }
    }
}

而迷宫的最短路径只需要把路径都搜完，取最短的一条就可以了

---

4.排列组合问题

关于排列组合的问题，可参考https://www.bcoi.cn/blog/327/67e74b09ad38ea3dd8777424#1743211273212 。

但是这里不讲排列组合的公式，我们要讲的是DFS实现排列组合。如果要求再[1, 2, 3]中选2个数排列，我们很清楚有6种可能：[1, 2]，[1, 3]，[2, 1]，[2, 3]，[3, 1]，[3, 2]。可是怎么用DFS实现呢？可以这样想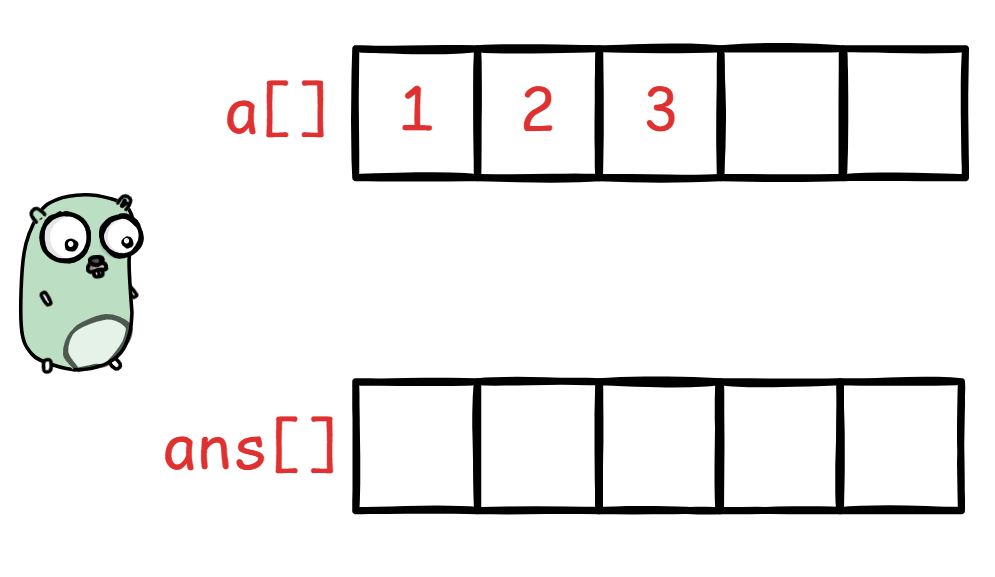： 小拨鼠要从a[]把数字搬到ans[]中，一次可以搬一个数字，选过一个数之后就打上标记，再选下一个数...一直到选完2（排列公式中的r）个。然后你就得到了排列的代码：

#include <iostream>
using namespace std;
int n,r,a[1005],ans[1005],used[1005];
void print()
{
    for (int i = 1; i <= r; i++)
        cout << ans[i] << " ";
    cout << "\n";
}
void dfs(int k)
{
    if (k > r)
    {
        print();
        return;
    }
    for (int i = 1; i <= n; i++)
    {
        if (used[i] == 0)
        {
            ans[k] = a[i];
            k++;
            used[i] = 1;
            dfs(k);
            used[i] = 0;
            k--;
            ans[k] = 0;
        }
    }
}
int main()
{
    cin >> n >> r;
    for (int i = 1; i <= n; i++)a[i] = i;
    dfs(1);
    return 0;
}

解决了排列，那组合呢？仔细想想，组合就是不重复的排列。小拨鼠这次选了第i个数，下次从第i个数开始选（应为打了标记，所以不会重复）是不是就不会重复了呢？于是你就得到了组合的代码：

void dfs(int k,int p)
{
    if (k > r)
    {
        print();
        return;
    }
    for (int i = p; i <= n; i++)
    {
        ans[k] = a[i];
        k++;
        dfs(k,i + 1);
        k--;
        ans[k] = 0;
    }
}

---

5.综合DFS

综合，就是综合嘛

---

6.DFS简单优化和剪枝

简单优化，这里只讲（D老师也只将了）记忆化剪枝。借助小拨鼠来理解：

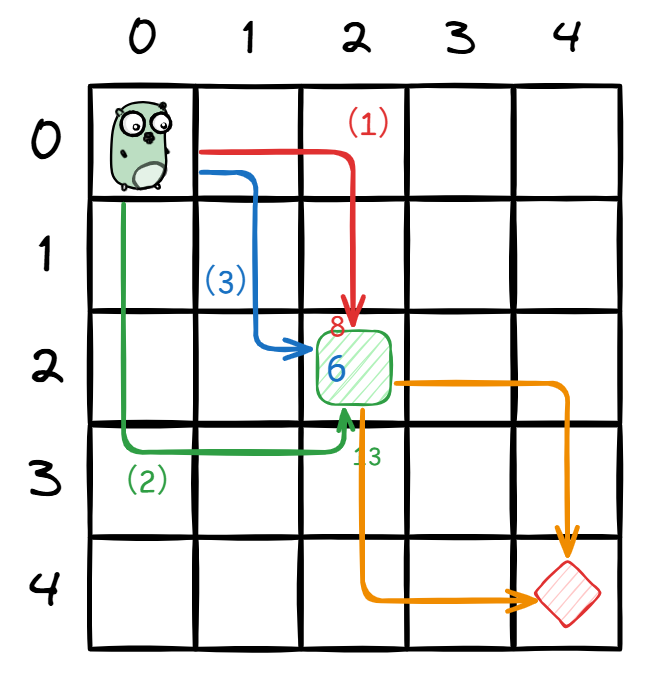
小拨鼠从(0,0)出发，要去(4,4)，在(2,2)有笔记本（实际上每个格子上都有笔记本）可以记录来到这里的最短路径。

第一条路，第一次到笔记本，路径长度为8，比笔记本原有的数 （笔记本每个格子都要初始化一个极大值） 小，更新笔记本为8；

第二条路，路径长度为13，不更新笔记本，也不继续搜索，直接return；

第三条路，路径长度为6，更新笔记本......

于是你就得到了记忆化的代码：

if (f[x][y] <= cnt)return ;
f[x][y] = cnt;

不要看它只有两行，但可以超级加速！一道经典的BFS题目（建议用普通DFS、记忆化DFS和BFS分别实现，体会普通和记忆化DFS的时间差）骑士牛