背景

D老师又布置比赛了，这是GFHD欢度五一信奥赛B阶中的一道题

---

题目

---

题目背景

D老师出题伤了好多脑细胞啊

题目描述

虽然bcoi中有很多题目，但是想要选出一套最优的出题方案真的很伤脑筋。

假设bcoi题库中有 $n$ 道题目，现在有 $m$ 位同学参加比赛。

• 如果 $a_{i,j}=0$ ,表示第 $i$位同学没做过第 $j$道题。
• 如果 $a_{i,j}=1$ ,表示第 $i$位同学做过第 $j$道题。

D老师 想要从 $n$ 道题中挑 $4$ 道来组一套题，并且需要保证所有同学都最多只做过 $4$ 道题中的一道（每个人做过的可以不同），请问有多少种选择方法。

输入格式

两个数 $n,m$。

接下来有 $m$ 行，每行 $n$ 个数，第 $i$ 行第 $j$ 个数为 $a_{i,j}$ 。

输出格式

一个整数，表示组题的方案数。

Sample Input 1

5 2 
1 0 0 0 0
1 0 1 0 0

Sample Output 1

2

两种选择方法如下，o 表示选择，x 表示不选择。

1 0 0 0 0
1 0 1 0 0
---------
o o x o o
x o o o o

Sample Input 2

4 3
0 0 0 0
1 1 0 0
0 1 0 0

Sample Output 2

0

当然也有没有方案的情况。

Sample Input 3

4 5
0 0 0 0
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

Sample Output 3

1

自然也有唯一解的情况。

数据规模与约定

对于 $100$ 的数据，$4≤n≤88$, $1≤m≤1000$.

• 子任务 1（10 分）：保证 $n=4$
• 子任务 2（20 分）：保证 $m=1$
• 子任务 3（30 分）：保证 $n^4×m×4≤10^8$。
• 子任务 4（40 分）：没有特殊限制。

---

题解

---

题解背景

同学们做题伤了好多脑细胞啊

。。。

好吧，开始看题目。嗯，从 $n$ 道题中选出 $4$ 道题。一看就是 DFS 的排列组合嘛，这简单！

#include <iostream>
using namespace std;
int n, m, a[1005][1005], ans, pro[1005];
bool check()
{
    for (int im = 1; im <= m; im++)
    {
        int sn = 0;
        for (int i = 1; i <= n; i++)
        {
            if (pro[i] == 1 && a[im][i] == 1)sn++;
            if (sn > 1)return 0;
        }
    }
    return 1;
}
void dfs(int k, int rn)
{
    if (k > n)
    {
        if (rn == 4 && check())ans++;
        return ;
    }
    if (rn > 4)return ;
    for (int i = 0; i <= 1; i++)
    {
        pro[k] = i;
        dfs(k + 1, rn + i);
        pro[k] = 0;
    }
}
int main()
{
    freopen("yi.in", "r", stdin);
    freopen("yi.out", "w", stdout);

    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            cin >> a[i][j];
        }
    }
    dfs(1, 0);
    cout << ans;
    return 0;
}

好吧， 60 Time Exceeded 。DFS不行，肯定是递归太多层了，才导致超时（其实也就4层）。那DFS不行，我for*for*for*for（四层for循环）遍历每道题目总行了吧。

#include <iostream>
using namespace std;
int n, m, a[1005][1005], ans;
bool check(int p1, int p2, int p3, int p4)
{
    for (int i = 1; i <= m; i++)
    {
        int cnt = a[i][p1] + a[i][p2] + a[i][p3] + a[i][p4];
        if (cnt > 1) return 0;
    }
    return 1;
}
int main()
{
	freopen("yi.in", "r", stdin);
    freopen("yi.out", "w", stdout);
	ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
	
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			cin >> a[i][j];
		}
	}
	
	for (int p1 = 1; p1 <= n; p1++)
	{
		for (int p2 = p1 + 1; p2 <= n; p2++)
		{
			for (int p3 = p2 + 1; p3 <= n; p3++)
			{
				for (int p4 = p3 + 1; p4 <= n; p4++)
				{
					if (check(p1, p2, p3, p4))ans++;
				}
			}
		}
	}
	cout << ans;
	return 0;
}

60 Time Exceeded。。。我还优化了 check() 和输入输出呢！！

剩下40分怎么得呢

按照样例1，把所有题目的排列都列出来，如图：

这有什么规律呢？

如果把第一列和第三列框起来，我们可以发现，如果同时拥有一和三的排列都是不可行的，如样例1所示

5 2 
1 0 0 0 0
1 0 1 0 0

发现第二个同学做出了第一题和第三题，所以只要有第一题和第三题的题目排列，第二个同学就可以做出两道题，不符合题目。如果把发现转换成表格，就会有：

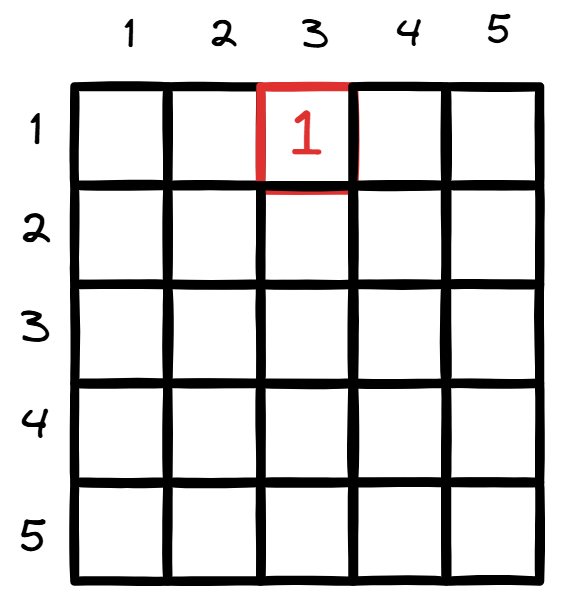
其实在 [3][1] 的位置也应该是 1 。

怎么填这个表格呢？肯定要用 $i$ 和 $j$ 来判断两道题目，再用一个变量来判断每一位同学（应为只要有一位同学同时做过第 $i$ 题和第 $j$ 题，就不能选）。如此就可以填好表格了：

for (int ti = 1; ti <= m; ti++)
{
    for (int i = 1; i < n; i++)
    {
        for (int j = i + 1; j <= n; j++)
        {
            if (a[ti][i] && a[ti][j])che[i][j] = 1;
        }
    }
}

a 数组就是输入， che (check) 就是上面的表格。

如此，填好表格。在 DFS 或是四层 for 循环时，直接跳过有冲突的排列。

题解：

最佳出题方案

当然，你也可以用（如果可以想到）其他方法，例如...（VIP内容）...

---

100 Accepted!