背景

这个点子是在洗澡的时候想出来的（奇怪的点子总是这个时候冒出来）：把 BFS 的队列改成栈会怎样？

因为D老师说过递归的调用是用栈来实现的，所以联想到 DFS 。

---

搜索算法

如果你没有学过搜索： DFS 、 BFS 。

（以下内容选择生物课本，有删改）

实验 · 探究

实验 · 探究：用栈实现 BFS。

提出问题

用栈实现 BFS 是怎样的搜索顺序？

作出假设

结合下面的材料，做出假设

BFS 使用队列实现，有先进先出（FIFO）的特点；

DFS 使用递归实现，内部使用栈实现，有先进后出（FILO）的特点。

假设：可能是 BFS 和 DFS 的结合，但既不是 BFS ，也不是 DFS 。

制定计划

怎样通过实验检验我的假设呢？

1. 找到 BFS 的模板题：快乐的马里奥 。
2. 分别使用 BFS（队列）、 BFS（栈）、DFS实现。需要保证其他变量相同且适宜。

实施计划

BFS（队列）

首先用 BFS 做。核心代码：

void bfs()
{
	queue <stu> q;
	q.push(stu{1, 1, num});
	while (q.size() != 0)
	{
		stu f = q.front();
		q.pop();
		if (num - 1 == n * m)
		{
			return;
		}
		for (int i = 1; i <= 4; i++)
		{
			int nx = f.x + dx[i];
			int ny = f.y + dy[i];
			if (check(nx, ny))
			{
				a[nx][ny] = num++;
				q.push(stu{nx, ny, num});
			}
		}
	}
}

对于样例，输出：

1 2 4
3 5 7
6 8 9

它的遍历方式是：

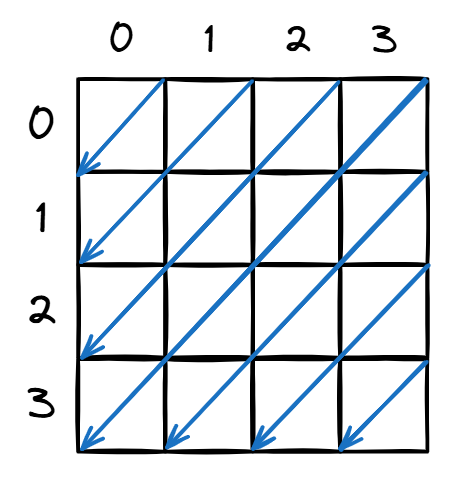
DFS

核心代码：

void dfs(int x, int y)
{
	if (num - 1 == n * m)return ;
	for (int i = 1; i <= 4; i++)
	{
		int nx = x + dx[i];
		int ny = y + dy[i];
		if (check(nx, ny))
		{
			a[nx][ny] = num++;
			dfs(nx, ny);
		}
	}
}

输出：

1 2 3 
8 9 4 
7 6 5 

可以发现，它有点像螺旋。但实际上不是的。它的遍历方式是：

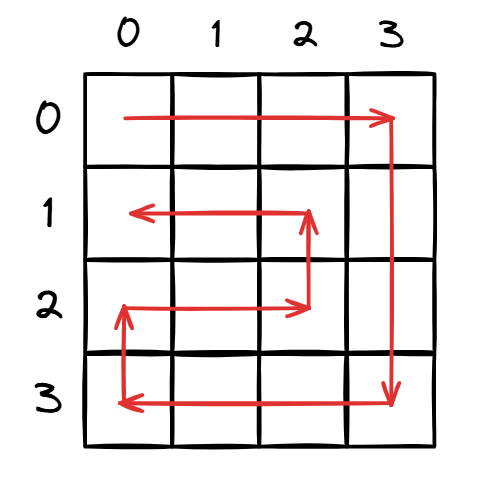
BFS（栈）

只需要把 BFS（队列）的所有 queue 改成 stack ，所有 front 改成 top 。核心代码：

void bfs()
{
	stack <stu> q;
	q.push(stu{1, 1, num});
	while (q.size() != 0)
	{
		stu f = q.top();
		q.pop();
		if (num - 1 == n * m)
		{
			return;
		}
		for (int i = 1; i <= 4; i++)
		{
			int nx = f.x + dx[i];
			int ny = f.y + dy[i];
			if (check(nx, ny))
			{
				a[nx][ny] = num++;
				q.push(stu{nx, ny, num});
			}
		}
	}
}

输出：

1 2 9 
3 4 8 
5 6 7 

让我探究一下它的遍历顺序。

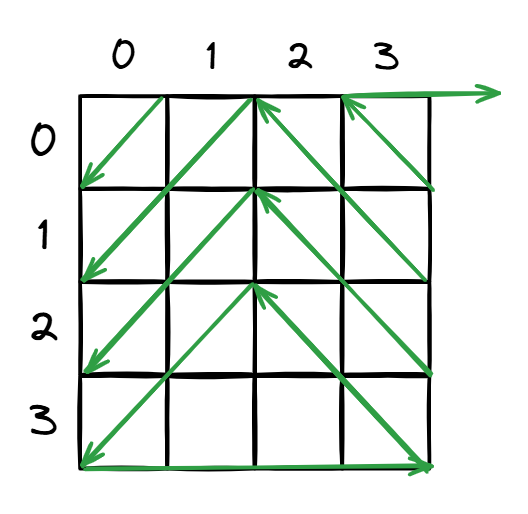
额……

分析结果，得出结论

额……这就很烧脑了。每一个的结果都是不一样的。再用另一题吧。BFS 专属题目：骑士牛

BFS（队列）

使用标准 BFS 可以很快地求出答案。核心代码：

void bfs()
{
	queue <stu> q;
	q.push(stu{sx, sy, 0});
	while (q.size() != 0)
	{
		stu f = q.front();
		q.pop();
		if (f.x == ex && f.y == ey)
		{
			cnt = f.step;
			return;
		}
		for (int i = 1; i <= 8; i++)
		{
			int nx = f.x + dx[i];
			int ny = f.y + dy[i];
			if (check(nx, ny))
			{
				map[nx][ny] = 1;
				q.push(stu{nx, ny, f.step + 1});
			}
		}
	}
	return;
}

DFS + 记忆化

核心代码：

void dfs(int x, int y)
{
	if (x == ex && y == ey)
	{
		ans = min(ans, cnt);
		return ;
	}

	if (f[x][y] <= cnt)return ;
	f[x][y] = cnt;

	for (int i = 1; i <= 8; i++)
	{
		int nx = x + dx[i];
		int ny = y + dy[i];
		if (check(nx, ny))
		{
			map[nx][ny] = 1;
			cnt++;
			dfs(nx, ny);
			cnt--;
			map[nx][ny] = 0;
		}
	}
}

加了记忆化可以 AC，但是较慢。

BFS（栈）

核心代码：

void bfs()
{
	stack <stu> q;
	q.push(stu{sx, sy, 0});
	while (q.size() != 0)
	{
		stu f = q.top();
		q.pop();
		if (f.x == ex && f.y == ey)
		{
			cnt = f.step;
			return;
		}
		for (int i = 1; i <= 8; i++)
		{
			int nx = f.x + dx[i];
			int ny = f.y + dy[i];
			if (check(nx, ny))
			{
				map[nx][ny] = 1;
				q.push(stu{nx, ny, f.step + 1});
			}
		}
	}
	return;
}

不会 TLE， 但是 WA了。其实如果 DFS 也一搜到就直接 return 的话也不会 TLE。

只能说BFS（栈）即没有 BFS 的高效，也没有 DFS 的简洁。

既然 DFS 叫大法师， BFS 叫冰法师，而这是 DFS 和 BFS 的结合，就叫它 DBS 吧（大鼻屎）。

还是请教一下 DeePseek 吧。（以下是D...P...解析）

---

BFS使用队列、BFS使用栈与DFS的比较

基本概念

1. 正常BFS（使用队列）

• 数据结构：队列（FIFO）
• 遍历顺序：逐层扩展，先访问离起点近的节点
• 空间复杂度：O(b^d)（b是分支因子，d是深度）
• 完备性：是（在有限图中能找到解）

2. "BFS"使用栈（实际上是类DFS行为）

• 数据结构：栈（LIFO）
• 遍历顺序：会变成类似深度优先的行为，但访问顺序与DFS不同
• 空间复杂度：O(bd)
• 完备性：是（在有限图中能找到解）

3. DFS

• 数据结构：栈（LIFO）
• 遍历顺序：沿一条路径深入到底，然后回溯
• 空间复杂度：O(bd)
• 完备性：在无限图中不完备（可能陷入无限分支）

区别与联系

特性	队列BFS	栈"BFS"	DFS
数据结构	队列(FIFO)	栈(LIFO)
遍历顺序	层级顺序	类似DFS但顺序不同	深度优先
空间复杂度	O(b^d)	O(bd)
完备性	是		无限图中否
最短路径	能找到	不能保证

代码示例对比

略。

关键区别

1. 遍历顺序：

   • 队列BFS：按距离起点层级递增的顺序访问
   • 栈"BFS"：会先访问最后加入的邻居，行为类似DFS但不完全相同
   • DFS：沿着一条路径深入到底

2. 最短路径：

   • 只有队列BFS能保证找到无权图的最短路径
   • 栈"BFS"和DFS不能保证

3. 空间效率：

   • 队列BFS在最坏情况下空间需求更大
   • 栈"BFS"和DFS空间效率更高

栈实现的"BFS"实际上是一种变体的DFS，它失去了BFS的核心特性（层级遍历和最短路径保证），但保留了DFS的空间效率。这种实现很少在实际中使用，因为它结合了两者的缺点而没有明显优势。

---

（以上是解析）

😂👌真的有点________……