说明

这篇 blog 分为线性 DP 和背包 DP。

---

一、线性 DP

详细

动态规划（简称 DP ）是一种思想。它把问题分解为多个子问题，逐个求解。

（一）、DP 与分治、贪心的异同点

相同点

DP 、分治和贪心都是分解子问题，逐个求解。

不同点

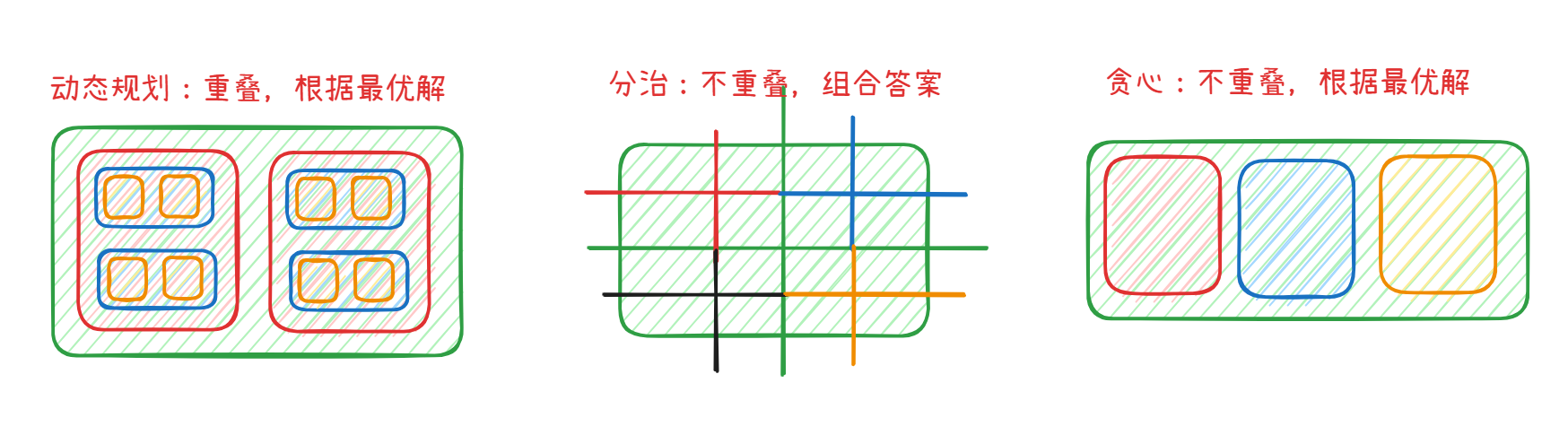
DP 是将问题分解为重叠的子问题，再根据子问题的最优解得到整体的最优解。如果子问题不重叠，就体现不出 DP 的优势。

分治是将问题分解为不重叠的子问题，再将子问题分解为子问题的子问题，组合得到答案。

贪心是将问题分解为不重叠的子问题，根据子问题的最优解得到整体的最优解。

如下图：

（二）、DP 的三个性质

1. 无后效性
2. 最优子结构
3. 重叠子问题

（三）、解决 DP 的五个步骤

1. 分析问题
2. 定义状态变量
3. 设计状态转移方程
4. 设置初始状态和边界
5. 确定答案

---

二、背包 DP

还是 D 老师讲的好。

顾名思义，背包 DP 的意思就是装物品进背包。题目大概是这样的：小拨鼠有一个背包，有一些物品。这些物品各有重量和价值。求小拨鼠在背包装得下的情况下最多能拿到多少价值。

其实背包 DP 还分为 01 背包、完全背包、混合背包、分组背包……今天（或者说昨天）学的只是 01 背包，即每件物品只有选和不选两种选择。

（一）、引入

还是看例题吧：01 背包问题 。

1. 贪心

先尝试用贪心做这道题。可以考虑到的贪心有三种：

1. 按重量从小到大排序，尽量装重量小的。
2. 按价值从大到小排序，尽量装价值大的。
3. 按性价比（$重量 : 价值$）从大到小排序，尽量装性价比大的。

代码：

#include <iostream>
#include <algorithm>
using namespace std;

struct stu
{
	int w, c;
}a[205];
int n, v, ans, wnt, cnt;

bool cmp1(stu x, stu y)
{
	return x.w < y.w;
}

bool cmp2(stu x, stu y)
{
	return x.c > y.c;
}

bool cmp3(stu x, stu y)
{
	return x.w * y.c > y.w * x.c;
}

int main()
{
	cin >> v >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i].w >> a[i].c;
	}
	
	// 贪心1：按重量从小到大排序
	wnt = cnt = 0;
	sort(a + 1, a + n + 1, cmp1);
	for (int i = 1; i <= n; i++)
	{
		if (wnt + a[i].w <= v)
		{
			wnt += a[i].w;
			cnt += a[i].c;
		}
	}
	ans = max(ans, cnt);

	// 贪心2：按价值从大到小排序
	wnt = cnt = 0;
	sort(a + 1, a + n + 1, cmp2);
	for (int i = 1; i <= n; i++)
	{
		if (wnt + a[i].w <= v)
		{
			wnt += a[i].w;
			cnt += a[i].c;
		}
	}
	ans = max(ans, cnt);

	// 贪心3：按性价比从大到小排序
	wnt = cnt = 0;
	sort(a + 1, a + n + 1, cmp3);
	for (int i = 1; i <= n; i++)
	{
		if (wnt + a[i].w <= v)
		{
			wnt += a[i].w;
			cnt += a[i].c;
		}
	}
	ans = max(ans, cnt);

	cout << ans;
	
	return 0;
}

只拿到了 80 分。看来贪心是不行的。但是误差都较小。

DFS 枚举

每一种物品都有选和不选两中状态。可以考虑用 DFS 来枚举每一种选择。代码：

#include <iostream>
using namespace std;
int n, m, w[35], c[35], ans;
void dfs(int k, int p, int wnt, int cnt)
{
	if (wnt > m)return ;
	if (k > n)return ;
	
	ans = max(ans, cnt);

	for (int i = p + 1; i <= n; i++)
	{
		dfs(k + 1, i, wnt + w[i], cnt + c[i]);
	}
}
int main()
{
	cin >> m >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> w[i] >> c[i];
	}
	dfs(0, 0, 0, 0);
	cout << ans;
	return 0;
}

可以 AC 。因为重量大于 $V$ 了就直接 return 。但是 DFS 也不好，如果物品数超过 $30$ ，就 TLE 了。

循环枚举

如果用 $0$ 表示不选这个物品， $1$ 表示选这个物品，那么把每一个物品的状态连成一串，就变成了一个二进制。例如物品数为 $2$ 时：

而且，这些二进制正好在十进制下是连续的。又例如有 $4$ 件物品：

最多的状态是： 全部都是一，即 (1<<n)-1 。当物品数为 $4$ 时， 1<<n 为 0001 0000 ，减一就为 0000 1111 。代码：

#include <iostream>
#include <algorithm>
using namespace std;

struct stu
{
	int w, c;
}a[205];
int n, v, ans, wnt, cnt;

int main()
{
	cin >> v >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i].w >> a[i].c;
	}
	
	for (int i = 0; i <= (1 << n) - 1; i++)
	{
		bool flag = 1;
		int t = i;
		wnt = cnt = 0;
		for (int j = 1; j <= n; j++)
		{
			if (t & 1)
			{
				wnt += a[j].w;
				cnt += a[j].c;
				if (wnt > v)
				{
					flag = 0;
					break;
				}
			}
			t >>= 1;
		}
		if (flag)ans = max(ans, cnt);
	}

	cout << ans;
	return 0;
}

可以 AC 。但是也有缺陷。一共有 $2^n$ 种状态，当 $n$ 超过某个值（反正不大）循环就会超时。或者，如果 $n$ 超过 $64$ 时（unsigned long long 的二进制位数），不要说 int 了， unsigned long long 都会溢出。

（二）、背包 DP 解法

既然上面的三种算法都有缺陷，下面就是考虑动态规划了。

1. 分析问题

（1）.无后效性

这有点烧脑。哪里有无后效性啊？难道选了这个物品之后就不能选前面的物品了吗？

（2）.最优子结构

选择每个物品时保证价值最大，就可以保证最终价值最大。

（3）.重叠子问题

选前 $2$ 个物品时，就要先计算选前 $1$ 个物品的最大价值。以此类推，每个子问题都是重叠的。

2. 定义状态变量

正向烧烤 can be difficult. 可以反推，从问题出发。

问题：选择 $n$ 个物品，背包容量为 $v$ 时的最大价值。
转换成数学公式：$f(n)(v)=S_{nv}$ ；
转化为通式： $f(i)(j)=S_{ij}$ ；
转化为数组：f[i][j] = S_ij 。

现在就有了数组的定义：选择前 $i$ 项物品，背包容量为 $j$ 时的最大价值。

3. 设计状态转移方程

对于每一个物品，都有选和不选两种状态。

（1）. 不选当前物品

dp[i][j] 任然和前 $i-1$ 个物品时相等。So, dp[i][j] = dp[i - 1][j] 。

（2）. 选当前物品

If 要选当前物品，那么首先要保证背包容量可以装的下当前物品，即 j >= w[i] 。

If 要选，还要先给这个物品留下空间，重量为 j - w[i] 。物品还是 $i-1$ 个。即 dp[i - 1][j - w[i]] 。还要加上装了的这个物品的价值。即 dp[i - 1][j - w[i]] + c[i] 。

取较大值。即 dp[i][j] = max(dp[i][j], dp[i - 1][j - w[i]] + c[i] 。

4. 设置初始状态和边界

当选择 $0$ 件物品，或背包容量为 $0$ 时装不了，价值为 $0$ 。这可以忽略 if 你定的是全局变量。

5. 确定答案

选前 $n$ 个物品，背包容量为 $v$ 时的最大价值。即 dp[n][v] 。

6. 代码

#include <iostream>
using namespace std;
int n, v, w[35], c[35], dp[205];
int main()
{
	cin >> v >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> w[i] >> c[i];
	}
	for (int i  = 1; i <= n; i++)
	{
		for (int j = v; j >= w[i]; j--)
		{
			dp[j] = max(dp[j], dp[j - w[i]] + c[i]);
		}
	}
	cout << dp[v];
	return 0;
}

三、空间压缩

通过观察，我们可以发现：每一次的运算只关系到前一排。所以可以压缩为二维。如果是偶数就用上一行的数据，反之就用下一行的数据。简单来说就是模上 $2$ 。代码：

#include <iostream>
using namespace std;
int n, v, w[35], c[35], dp[2][205];
int main()
{
	cin >> v >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> w[i] >> c[i];
	}
	for (int i  = 1; i <= n; i++)
	{
		for (int j = 0; j <= v; j++)
		{
			dp[i % 2][j] = dp[(i - 1) % 2][j];
			if (j >= w[i])
				dp[i % 2][j] = max(dp[i % 2][j], dp[(i - 1) % 2][j - w[i]] + c[i]);
		}
	}
	cout << dp[n % 2][v];
	return 0;
}

可以 AC 。

如果继续压缩呢。如图：

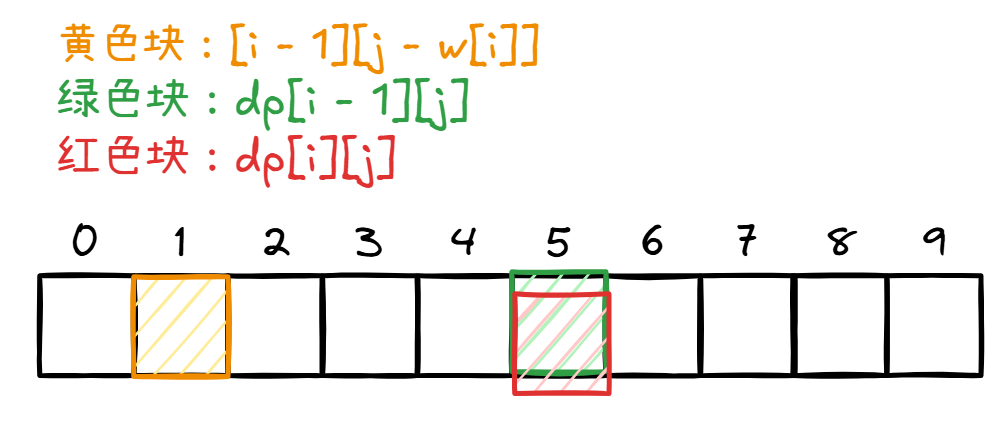
If 是顺序遍历的话，红色格子走过的地方就是这一轮的数据，但是黄色格子需要的是上一轮的数据。因此会造成重复选择，进化为变成完全背包。所以需要倒序。