说明

（没办法， D 老师还是讲快了）

终于能叫背包 DP 的全称了。

本文分为（按照 D 老师在 训练 里的分类）：

1. 01 背包
2. 满背包
3. 多维背包
4. 多重背包
5. 完全背包
6. 混合背包
7. 分组背包
8. 条件背包

如果有错误请指出。

---

01 背包

详细

01 背包的转移关于选和不选的状态，如图所示：

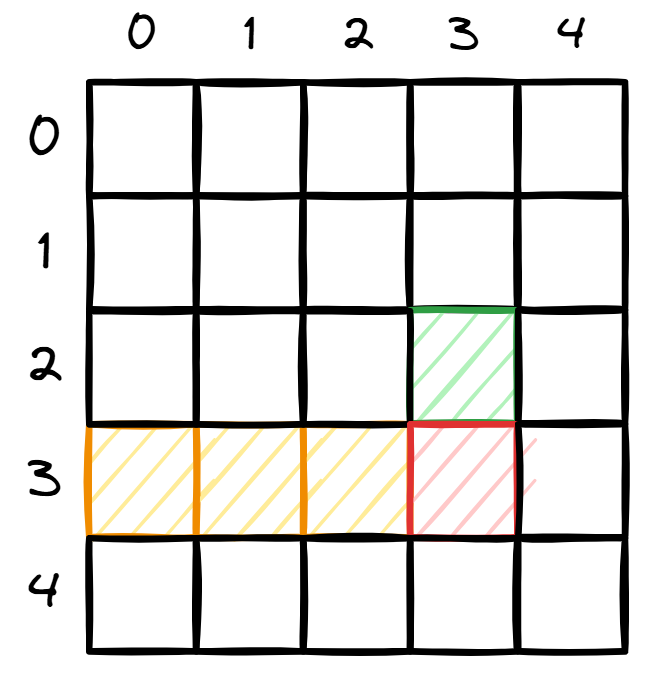
当前的状态（红色的格子）可以有选（橙色格子）和不选（绿色格子）转移而来。

核心代码（空间优化后）：

for (int i = 1; i <= n; i++)
{
	for (int j = m; j >= v[i]; j--)
	{
		dp[j] = max(dp[j], dp[j - v[i]] + c[i]);
	}
}
cout << dp[m];

例题：简单背包问题。

满背包

满背包是一种 01 背包的变形（什么背包不是呢？）

满背包就是看能不能装满背包。有两种方法：

1. 转化为 01 背包

其实满背包不会给你物品的价值。只需要把价值看成重量就好了。用 01 背包求最大价值，检查是否是背包容量。核心代码（空间优化后）：

for (int i = 1; i <= n; i++)
{
	for (int j = m; j >= v[i]; j--)
	{
		dp[j] = max(dp[j], dp[j - v[i]] + c[i]);
	}
}
cout << (dp[m] == m ? "YES" : "NO");

2. 优化

可以不用那么麻烦。定义 dp[i] 表示能否组成这个重量。再根据 01 背包的转移就好了。可以提前检查 dp[s] 是否为 true ，是的话直接结束。核心代码：

dp[0] = 1;
for (int i = 1; i <= n; i++)
{
	for (int j = m; j >= v[i]; j--)
	{
		dp[j] = dp[j] || dp[j - v[i]];
	}
	if (dp[m])
	{
		cout << "YES";
		return 0;
	}
}
cout << (dp[m] ? "YES" : "NO");

例题：简单背包问题。

多维背包

就是多维。（其实我也不是很懂）

例题：编辑距离。

多重背包

这种背包会给你每件物品的数量。只需要（对于 01 背包）加一个循环枚举物品的个数。核心代码：

for (int i = 1; i <= n; i++)
{
	for (int j = 0; j <= m; j++)
	{
		for (int k = 1; k <= num[i]; k++)
		{
			if (j >= v[i] * k)
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i] * k] + c[i] * k);
		}
	}
}
cout << dp[n][m];

也可以空间压缩：

for (int i = 1; i <= n; i++)
{
	for (int j = m; j >= 0; j--)
	{
		for (int k = 1; k <= num[i]; k++)
		{
			if (j >= v[i] * k)
				dp[j] = max(dp[j], dp[j - v[i] * k] + c[i] * k);
		}
	}
}
cout << dp[m];

例题：多重背包（1）

多重背包-优化

如果背包已经装不下 v[i] * k 的重量，可以直接结束。核心代码：

for (int i = 1; i <= n; i++)
{
	for (int j = m; j >= 0; j--)
	{
		for (int k = 1; k <= num[i]; k++)
		{
			if (j >= v[i] * k)
				dp[j] = max(dp[j], dp[j - v[i] * k] + c[i] * k);
			else break;
		}
	}
}
cout << dp[m];

例题：多重背包（2）

完全背包

这就有漫长的推导过程了。

完全背包就是每种物品都可以选无数个。首先想到的就是用一个循环枚举个数，直到背包装不下。如图：

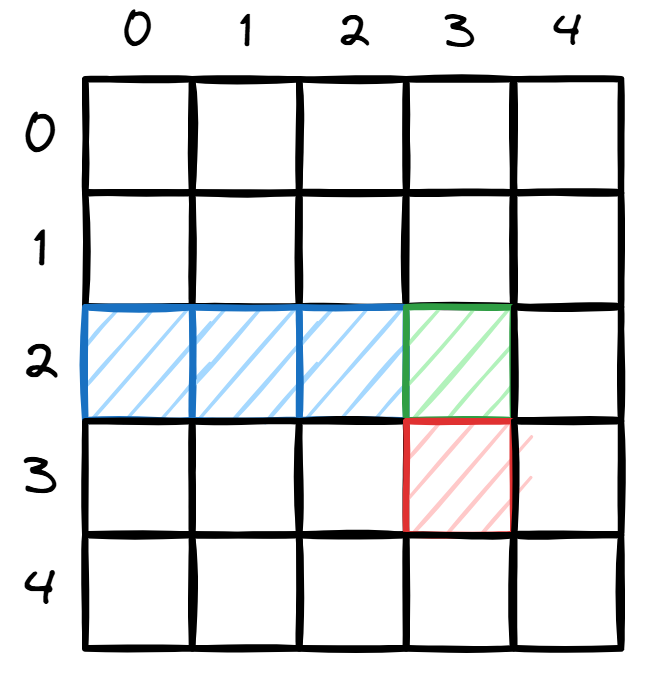
按照 01 背包的转移的状态，红色的格子可以有绿色或蓝色的格子转移而来。核心代码：

for (int i = 1; i <= n; i++)
{
	for (int j = 0; j <= m; j++)
	{
		for (int k = 1; j >= v[i] * k; k++)
		{
			dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i] * k] + c[i] * k);
		}
	}
}
cout << dp[n][m];

这里可以考虑优化：所有蓝色格子的最大价值就存储再红色格子的左边：

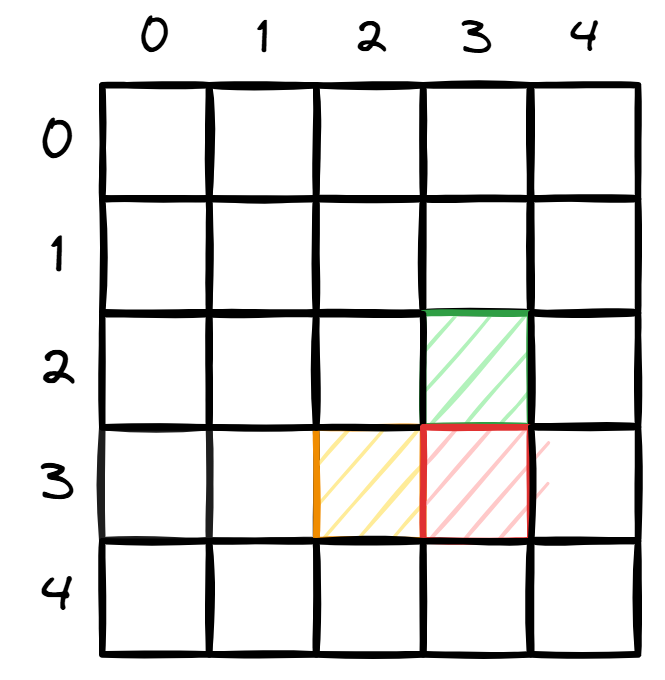
橙色格子就可以替代所有蓝色格子。核心代码：

for (int i = 1; i <= n; i++)
{
	for (int j = 0; j <= m; j++)
	{
		dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + c[i] * k);
	}
}
cout << dp[n][m];

完全背包-空间压缩

其实背包都可以空间压缩吧，包括多维背包。

类似（非常类似） 01 背包的空间压缩。 01 背包需要用到上一轮的橙色格子，如果顺序遍历的话会造成修改，使结果不正确，因此需要倒序。但是完全背包需要用的是这一轮的橙色格子，所以直接正序遍历就是完全背包的空间压缩。核心代码：

for (int i = 1; i <= n; i++)
{
	for (int j = 0; j <= m; j++)
	{
		dp[j] = max(dp[j], dp[j - v[i]] + c[i] * k);
	}
}
cout << dp[m];

例题：完全背包

混合背包

混合背包就是背包的混合。这个背包也会给你每件物品的数量，但和多重背包不同的是，它有些物品可以选择无数种。核心代码（空间压缩后）：

for (int i = 1; i <= n; i++)
{
	if (num[i] == 0)
	{
		for (int j = v[i]; j <= m; j++)
		{
			dp[j] = max(dp[j], dp[j - v[i]] + c[i]);
		}
	}
	else
	{
		for (int j = m; j >= 0; j--)
		{
			for (int k = 1; k <= num[i]; k++)
			{
				if (j >= v[i] * k)
					dp[j] = max(dp[j], dp[j - v[i] * k] + c[i] * k);
				else break;
			}
		}
	}
}
cout << dp[m];

（因该没错吧？太长了）

分组背包

分组背包就是给物品分组。每组物品只能选一个物品。核心代码：

for (int i = 1; i <= n; i++)
{
    for (int j = 1; j <= m; j++)
    {
        dp[i][j] = dp[i - 1][j];
        for (int k = 1; k <= s[i]; k++)
        {
            if (j >= v[i][k])
            {
                dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i][k]] + w[i][k]);
            }
        }
    }
}
cout << dp[n][m];

条件背包

条件背包就是附加了条件。例如要买 A 物品，就必须买 B 物品。