前言

这一块就有好讲的了。如果有问题请指出。

目录：

素数

• 素数的判定
• 素数的筛法

GCD

• GCD&LCM
• 扩展欧几里得
• 丢番图方程
• 裴蜀定理

斐波那契数列

---

素数 ^[1]

这是很大很重要又很简单的一部分（算简单的了）。

定义： 素数（又称质数）是指除了 $1$ 和本身之外没有其他因数的数。例如 $2,3,5,7$ 等。注意：$1$ 不是素数。

素数的判定 ^[2]

首先，要看素数的定义：

定义： 素数（又称质数）是指除了 $1$ 和本身之外没有其他因数的数。例如 $2,3,5,7$ 等。注意：$1$ 不是素数。

因此，可以设计一个算法，枚举从 $2$ 到 $n - 1$ 的数字，检查是否能整除 $n$ 。如果可以，则说明 $n$ 是合数。如果都没有，则说明 $n$ 为素数。代码如下：

bool isp(int n)
{
	if (n < 2)return 0;
	for (int i = 2; i < n; i++)
	{
		if (n % i == 0)return 0;
	}
	return 1;
}

需要注意 $1$ 不是素数。

时间复杂度： $O(n)$ 。但是这并不高效（线性筛在这点时间能求 $n$ 个数，这个只能求 $1$ 个数你好意思吗）。

这样考虑： $n$ 的因子都是成对出现的（自动忽略平方数），而且每一对都有较大和较小。只需要在 $n$ 的一半中找到 $n$ 的较小的因子就好了。代码：

bool isp(int n)
{
	if (n < 2)return 0;
	int a = n / 2;
	for (int i = 2; i <= a; i++)
	{
		if (n % i == 0)return 0;
	}
	return 1;
}

这样就优化到了 $O(\frac{n}{2})$ 。但是还不够高效。

假设 $n$ 不是平方数。因为 $n$ 的因子都是成对出现的，所以我们可以把 $n$ 的因子分为 $2$ 部分：

1. 较小的因子；
2. 较大的因子。

但是“较”是不确定的，需要求解。设 $a$ 为“较小的因子”中最大的，那么 $\frac{n}{a} > a$ ，且 $a^2$ 十分接近 $n$ 。设 $b$ 为 $n$ 的因子中比 $a$ 更大的因子。假设 $b^2$ 也小于 $n$ ，那么 $\frac{n}{b}$ 一定会小于 $b$ 。但这与 “$a$ 为‘较小的因子’中最大的”冲突。

这下“较小”和“较大”的分解线就明确了： $\sqrt{n}$ 。举一个简单的例子。这是 $100$ 的所有因子：

$$1 \times 100 \\ 2 \times 50 \\ 4 \times 25 \\ 5 \times 20 \\ 10 \times 10 \\ 20 \times 5 \\ 25 \times 4 \\ 50 \times 2 \\ 100 \times 1 $$

可以发现， $10$ 就是 $100$ 的因子中“较小的因子”的最大的。如果 $n$ 没有“较小的因子”，那么 $n$ 也不会有“较大的因子”。于是可以优化判断素数的代码，只需要循环到 $\sqrt{n}$ 。时间复杂度： $O(\sqrt{n})$ 。代码：

bool isp(int n)
{
	if (n < 2)return 0;
	int a = sqrt(n);
	for (int i = 2; i <= a; i++)
	{
		if (n % i == 0)return 0;
	}
	return 1;
}

还可以继续优化。先判断是否是偶数，后面只循环奇数。时间复杂度： $O(\frac{\sqrt{n}}{2})$ 。代码：

bool isp(int n)
{
	if (n == 2)return 1;
	if (n < 2 || n % 2 == 0)return 0;
	int a = sqrt(n);
	for (int i = 3; i <= a; i += 2)
	{
		if (n % i == 0)return 0;
	}
	return 1;
}

其实还可以继续优化，但是会非常麻烦。理想最优解：只循环素数。

素数的筛法 ^[3]

概念： 利用某个基数，它的倍数都是合数，所以都筛掉。

素数筛1-普通筛

按照上面的方法。用两层循环模拟基数和倍数。注意不要出界。时间复杂度： $O(n \log{n})$ （因为倍数是倍增的）。代码：

int n, pre[N], top;
bool isp[N];
void make()
{
	isp[0] = isp[1] = 1;
	for (int i = 2; i <= n; i++)
	{
		if (!isp[i])pre[++top] = i;
		for (int j = i; j <= n; j += i)
		{
			isp[j] = 1;
		}
	}
}

素数筛2-埃氏筛

埃氏筛是对于普通筛的优化。对于普通筛有两种优化方式。

埃氏筛A

1. 例如 $4$ 的倍数肯定已经被 $2$ 的倍数筛过了，所以可以只筛素数。
2. 由于前 $i$ ~ $i \times(i-1)$ 已经被筛过了，所以 $j$ 循环可以从 $i * i$ 开始。

时间复杂度： $O(n \log{\log{n}})$ 。代码：

int n, pre[N], top;
bool isp[N];
void make()
{
	isp[0] = isp[1] = 1;//这里为了方便实际上标记的是合数 
	for (int i = 2; i <= n; i++)
	{
		if (!isp[i])
		{
			pre[++top] = i;
			for (int j = i * i; j <= n; j += i)
			{
				isp[j] = 1;
			}
		}
	}
}

埃氏筛B

$i$ 不再是枚举基数了，而是枚举倍数。对基数的枚举在 pre 和 $j$ 循环中。简单来说：用 $i$ 循环枚举倍数， $j$ 循环在 pre[] 中枚举基数。时间复杂度： $O(n \log{\log{n}})$ 。代码：

int n, pre[N], top;
bool isp[N];
void make()
{
	isp[0] = isp[1] = 1;//这里为了方便实际上标记的是合数 
	for (int i = 2; i <= n; i++)
	{
		if (!isp[i])pre[++top] = i;
		for (int j = 1; j <= top; j++)
		{
			if (i * pre[j] > n)break;//防止出界 
			isp[i * pre[j]] = 1;
		}
	}
}

可以发现埃氏筛已经很快了，但是还是有重复的筛选。

埃氏筛Aa

这个埃氏筛 Aa 是对埃氏筛的一点没啥用的优化。如果不用存储素数的话，对于外层循环可以只枚举到 $\sqrt{n}$ 。

素数筛3-线性筛（欧拉筛）

线性筛（又称欧拉筛）是对埃氏筛 B 的优化。

线性筛的结论是保证每个数 $m$ 一定只能在他的最小素数因素的时候被筛掉例如 $24=2 \times 2 \times 2 \times 3=2 \times 12=3 \times 8$;

如果没有 if(i%prime[j]==0)break; 这句，那么当 $i=8$ 时候，根据 vis[iprime[j]] ，当 $j=1$ 时候先筛掉 $8 \times 2=16$ 这个数，然后当 $j=2$ 时候继续筛 $8 \times 3=24$ 这个数，然后筛 $8 \times 5=40$ ......

其中 $24$ 这个数在 $i=12,j=1(prime[1]值等于2)$ 即$12*2=24$ 时候又会被重复筛一次; $40$ 这个数在$i=20,j=1(prime[1]值等于2)$ 即$20 \times 2=40$ 时候又会被重复筛一次......

因为 if(i%prime[j]==0)break; 上述魔法语句的存在,当 $i=8,j=1(prime[1]值为2)$ 时候就会 break ，那么 $24$ 就不会在 $i=8,j=2(prime[2]值等于3)$ 的时候被筛掉，而是一定只会在 $i=12,j=1(prime[1]值等于2)$ 时候，即 $i \times prime[1]=12 \times 2$ 的时候被筛掉，所以当 $1<12$ 的时候，都筛不到 $24$ 这样就保证了，每一个数，有且仅有一次被筛到，而且一定是被它的最小质因数筛到，所以 $n$ 个数就最多是筛 $n$ 次，时间复杂度优化到了 $O(n)$ 。

原文链接：https://www.bcoi.cn/discuss/661faa104291ba6dd5355eff#1713606736407

原文的原文的链接：https://blog.csdn.net/Yuki_fx/article/details/115103663

代码：

int n, pre[N], top;
bool isp[N];
void make()
{
	isp[0] = isp[1] = 1;//这里为了方便实际上标记的是合数 
	for (int i = 2; i <= n; i++)
	{
		if (!isp[i])pre[++top] = i;
		for (int j = 1; j <= top; j++)
		{
			if (i * pre[j] > n)break;//防止出界 
			isp[i * pre[j]] = 1;
			if (i % pre[j] == 0)break;//这步是魔法 
		}
	}
}

如果用 vector 会简洁一些，但是时间可能会更长。

int n;
bool isp[N];
vector <int> pre;
void make()
{
	isp[0] = isp[1] = 1;//这里为了方便实际上标记的是合数 
	for (int i = 2; i <= n; i++)
	{
		if (!isp[i])pre.push_back(i);
		for (auto j : pre)
		{
			if (i * j > n)break;//防止出界 
			isp[i * j = 1;
			if (i % j == 0)break;//这步是魔法 
		}
	}
}

---

GCD ^[4]

这一块是又大又重要又很难的一块。你以为这一块只有最大公约数，实际上多得多。

GCD&LCM ^[5]

约数，就是因数。

公约数，就是几个数共有的约数。

最大公约数（GCD），就是几个数的共约数中最大的。

倍数、公倍数、最小公倍数（LCM）也差不多。

求 GCD 的方法

有两种方法：

1. 辗转相除法（欧几里得算法）；
2. 二进制算法；

辗转相除法： 证明略。

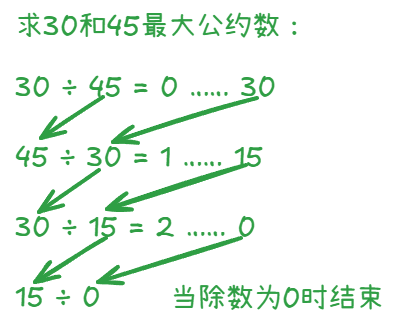
这比小学学的短除法快多了。很快可以发现，这可以用递归来实现。核心代码：

int gcd(int n, int m)
{
	if (m == 0)return n;
	return gcd(m, n % m);
}

二进制算法： 这是提高组的内容。

可以通过不断去除因子 $2$ 来降低常数。对于 $\gcd(x,y)$ ，分五种情况：

1. 若 $x=y$ ，则 $\gcd(x,y)=x=y$ 。
2. 若 $x、y$ 均为偶数， $\gcd(x,y)=2 \times \gcd(\frac{x}{2},\frac{y}{2})$ 。
3. 若 $x$ 为偶数， $y$ 为奇数， $\gcd(x,y)=\gcd(\frac{x}{2},y)$ 。
4. 若 $x$ 为奇数， $y$ 为偶数， $\gcd(x,y)=\gcd(x,\frac{y}{2})$ 。
5. 若 $x、y$ 均为奇数， $\gcd(x,y)=\gcd(x-y,y)$ 。

需要注意一些问题： $x-y$ 造成负数、运算符优先级等。代码（递归）：

int gcd(int x, int y)
{
	if (y == 0)return x;
	if (x == y)return x;
	if ((x & 1) == 0 && (y & 1) == 0)return gcd(x >> 1, y >> 1) << 1;
	if ((x & 1) == 1 && (y & 1) == 0)return gcd(x, y >> 1);
	if ((x & 1) == 0 && (y & 1) == 1)return gcd(x >> 1, y);
	if ((x & 1) == 1 && (y & 1) == 1)
	{
		if (x > y)return gcd(x - y, y);
		else return gcd(y - x, x);
	}
}

实际上辗转相除法和二进制 GCD 算法的时间复杂度都是 $O(\log \min (a,b))$ ，只是二进制 GCD 的位运算比辗转相除法的 % 运算更快。

求 LCM 的方法

求 LCM 也有两种方法：

1. 公式法。
2. 倍增法。

公式法： 只需要一点小小的推理。 我们知道： $a$ 和 $b$ 的最大公约数和最小公倍数的积等于 $a$ 和 $b$ 的积。那么：

$$gcd(a,b) \times lcm(a,b) = a \times b \\ lcm(a,b) = a \times b \div gcd(a,b) \\ $$

所以可以根据这个公式来推导 LCM 。时间复杂度： $O(\gcd)$ 。代码：

int lcm(int a, int b)
{
	return a * b / gcd(a, b);
}

倍增法： 倍增较大数，如果能被较小数整除，则为最小公倍数。时间复杂度： $O(\frac{b}{\gcd (a,b)})$ 。代码：

int lcm(int a, int b)
{
	if (a < b)a = a ^ b, b = a ^ b, a = a ^ b;//相当于swap(a,b); ，保证a>b 
	int i = 1;
	while (a * i % b != 0)
	{
		i++;
	}
	return a * i;
}

远不如公式法。

扩展欧几里得算法 ^[6]

扩展欧几里得算法（ ExGCD ），是用于根据一组 $(a,b)$ 求 $x$ 和 $y$ 使 $ax+by=\gcd(a,b)$ 成立的一组解。证明：

设 $a \times x_0 + b \times y_0 = \gcd(a, b) \\ b \times x_1 + (a \mod b) \times y_1 = \gcd(b, a \mod b) $ 。

根据欧几里得算法， $\gcd(a,b)=\gcd(b,a \mod b)$

所以 $a \times x_0 + b \times y_0 = b \times x_1 + (a \mod b) \times y_1$

而 $a \mod b = a - (\lfloor \frac{a}{b} \rfloor \times b)$

所以 $a \times x_0 + b \times y_0 = b \times x_1 + (a - \lfloor \frac{a}{b} \rfloor \times b) \times y_1$

去括号，得 $a \times x_0 + b \times y_0 = b \times x_1 + a \times y_1 - \lfloor \frac{a}{b} \rfloor \times b \times y_1$

合并同类项，得 $a \times x_0 + b \times y_0 = a \times y_1 + b \times(x_1 - \lfloor \frac{a}{b} \rfloor \times y_1)$

因为 $a = a, b = b$ ，所以左右两边同时除以 $a$ 和 $b$ ，得

$$x_0 = y_1 \\ y_0 = x_1 - \lfloor \frac{a}{b} \rfloor \times y_1 $$

利用引用技术，回溯时计算就好了。时间复杂度和欧几里得算法相同。代码：

int gcd(int a, int b, int& x, int& y)
{
	if (b == 0)
	{
		x = 1;
		y = 0;
		return a;
	}
	int ret = gcd(b, a % b, x, y);
	int x1 = x;
	x = y;
	y = x1 - (a / b) * y;
	return ret;
}

丢番图方程 ^[7]

丢番图方程，是形如这样的二元一次方程： $ax+by=c$ 。

补充：二元一次方程的定义

1. 含有两个未知数；
2. 含未知数的项的次数为一；
3. 是整式；
4. 是等式； （应该没了）

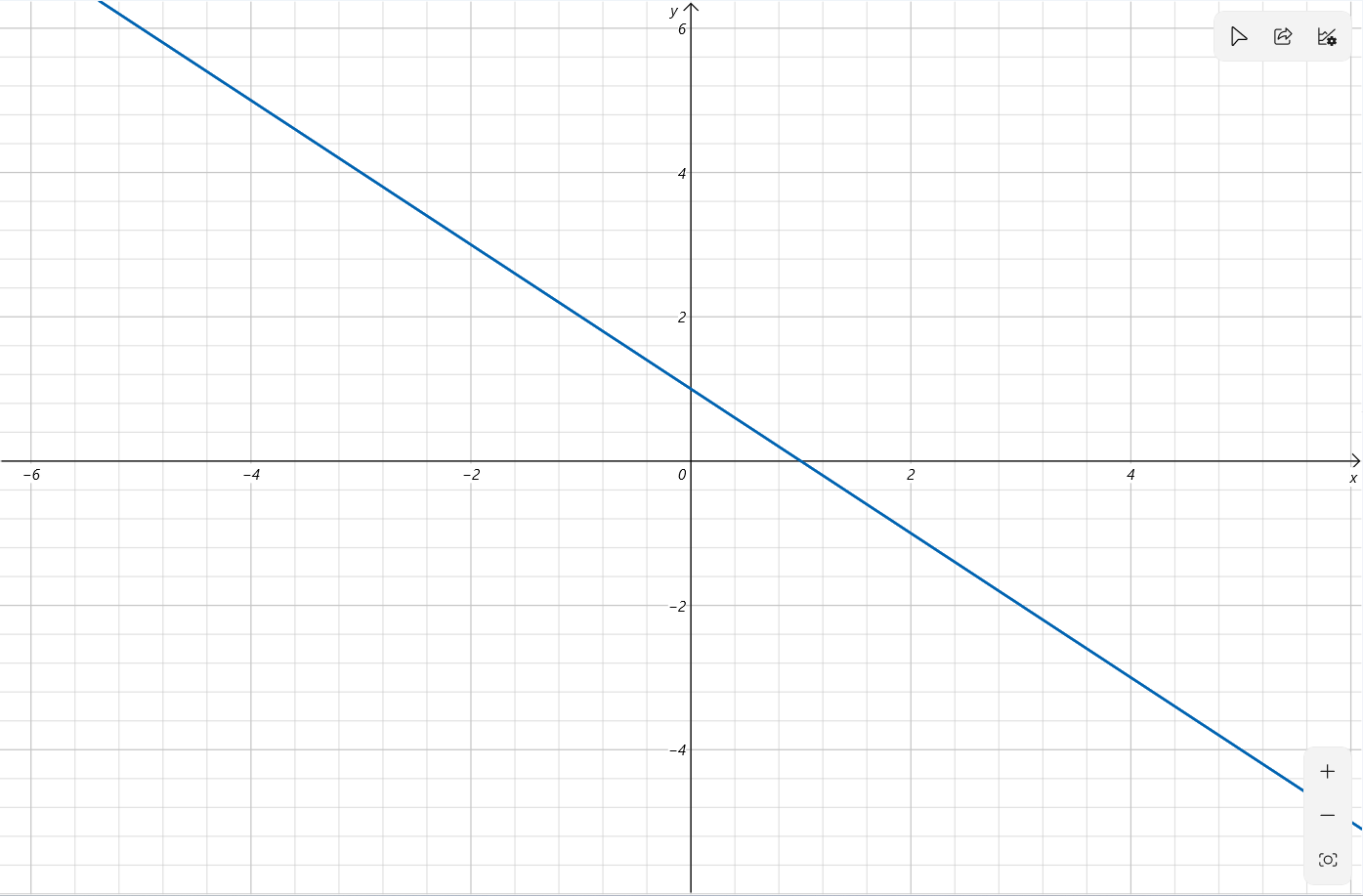
二元一次方程的函数图像为一条直线。例如这是 $x+y=1$ 的图像：

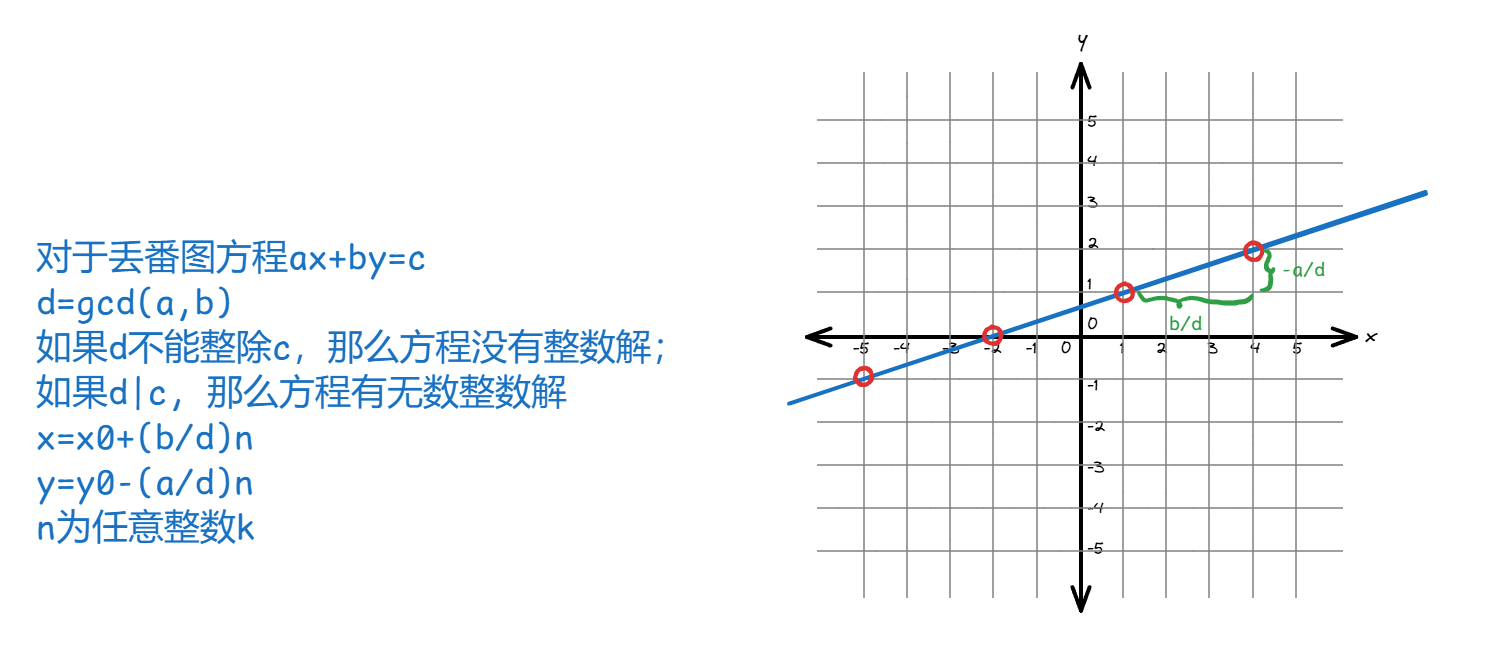
裴蜀定理 ^[8]

裴蜀定理，又称贝祖定理（Bézout's lemma）、贝祖等式（Bézout's identity）。是一个关于最大公约数的定理。 来源： https://oi-wiki.org/math/number-theory/bezouts/

裴蜀定理的内容是： 对于整数 $a$ 和 $b$ ，$∀ x,y \in \N$ ，满足 $\gcd(a,b)|ax+by$ ，且存在整数 $x$ 和 $y$ 使得 $ax+by=\gcd(a,b)$ 。

证明：略。

---

斐波那契数列 ^[9]

想不到吧！还有一块。 其实这部分不多。

定义： 斐波那契数列。又称黄金分割数列。它的前两项为 $1$ ，剩下每一项为前两项之和。这是斐波那契数列的前几项： $1,1,2,3,5,8,13......$ 。

递推方程： f[i] = f[i - 1] + f[i - 2] 。

通项式：

$$F(n) = \frac{\sqrt{5}}{5} × [(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n] $$

性质：

1. 前 n 项的和 = a[1]+a[2]+......+a[n] = 2a[n]+a[n-1]=a[n+2]-1
2. 奇数项和=a1+a3......+a[2n-1]=a[2*n]
3. 偶数项和=a2+......+a[2n]=a[2n+1]-1
4. 平方和=a1^2+a2^2+......+an^2=a[n]*a[n-1]
5. 中项：3a[i]=a[i-2]+a[i+2]

---

1. 素数 ↩︎

2. 素数的判定 ↩︎

3. 素数的筛法 ↩︎

4. GCD ↩︎

5. GCD&LCM ↩︎

6. 扩展欧几里得 ↩︎

7. 丢番图方程 ↩︎

8. 裴蜀定理 ↩︎

9. 斐波那契数列 ↩︎