前言^[1]

这篇 blog 又难又不详细而且没学过肯定听不懂。

目录：

• 前言
• 数论函数
• 欧拉函数

---

数论函数 ^[2]

数论函数是指定义域在正整数的函数。数论函数可以视为一个数列。

在数论函数中：

1. 若函数 $f(xy)=f(x)f(y)$ 在任意互质的 $x$ 和 $y$ 下成立，则称 $f(n)$ 为积性函数 ；
2. 若函数 $f(xy)=f(x)f(y)$ 在任意的 $x$ 和 $y$ 下成立，则称 $f(n)$ 为完全积性函数 ；

性质

积性函数的和函数也是积性函数。

和函数：例如函数 $f(n)$ ，它的和函数 $F(n)=\sum_{d|n}f(d)$ 。

欧拉函数 ^[3]

定义

欧拉函数 ，记作 $\varphi$ 。$\varphi(n)$ 指在 $[1,n]$ 中与 $n$ 互质的数的个数。

例如 $\varphi(1)=1$ 。当 $n$ 为质数时 $\varphi(n) = n-1$ 。

性质

看来还是要写证明。

• 欧拉函数是积性函数

  即对任意 $\gcd(a,b)=1$ 的整数 $a$ 和 $b$ ，有 $\varphi(ab)=\varphi(a)\varphi(b)$

  这就是积性函数的定义，没什么好讲的。

  特别的，当 $n$ 是奇数时， $\varphi(n)=\varphi(2n)$

  举个🌰：当 $n=9$ ：

  $$\varphi(2\times 9)=\varphi(2)\times\varphi(9) \\ \texttt{而} \varphi{2}=1 \texttt{,所以} \\ \varphi{(2\times 9)}=1\times\varphi(9)=\varphi(9) $$

  注意一定要满足 $n\texttt{为奇数}$ 。因为只有互质的 $x$ 和 $y$ 才能使 $\varphi(xy)=\varphi(x)\times\varphi(y)$ 。

• $n = \sum_{d|n}\varphi(d)$

  还是一个🌰：$12\texttt{的因子有：}1,2,3,4,6,12$.

  而

  $$ \varphi(1)+\varphi(2)+\varphi(3)+\varphi(4)+\varphi(6)+\varphi(12) \\ =1+1+2+2+2+4\\ =12\\ $$

  或者这样想：有 $n$ 个分数，分别是 $\frac{1}{n},\frac{2}{n},......,\frac{n}{n}$ 。其中有些分数可以化简。最后每一个分数 $\frac{a}{d}$ 都会有这些性质：

  • $d|n\texttt{(由于} d \texttt{是由} n \texttt{约分得到的)}$ 。
  • $a$ 和 $d$ 互质。
  • 分母为 $d$ 的数量就为 $\varphi(d)$ 个。因为如果还能约分就会一直往下，剩下不能约分的就是与 $d$ 互质的数，因此为 $\varphi(d)$ 。 这方面的🌰：
  

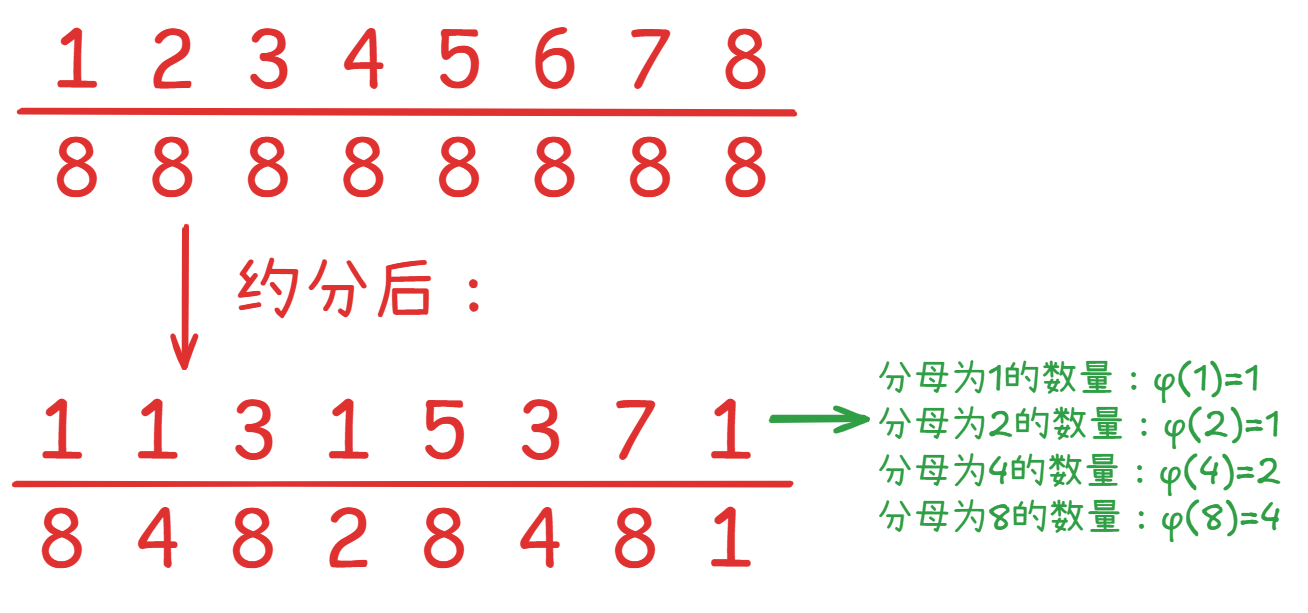
  由于总共有 $n$ 个数，而且上面所以有 $d$ 就是 $n$ 的所有因子，所以得到上面的结论。

• 若 $n=p^k$ ，其中 $p$ 是质数，那么 $\varphi(n)=p^k-p^{k-1}$

• 由唯一分解定理，设 $n = \prod_{i=1}^{s}p_i^{k_i}$ ，其中 $p_i$ 是质数，有 $\varphi(n) = n \times \prod_{i = 1}^s{\dfrac{p_i - 1}{p_i}}$ 。

  简单来说，就是把 $n$ 分解只因质因数，$\varphi(n)$ 就等于 $n$ 乘上 每个质因数 $P_i$ 的 $\frac{P_i-1}{P_i}$ 。

• 对任意不全为 $0$ 的整数 $m,n$ ，$\varphi(mn)\varphi(\gcd(m,n))=\varphi(m)\varphi(n)\gcd(m,n)$ 。

  可由上一条直接计算得出。

实现

这里目前 D 老师只讲了一种方法。

方法一：暴力法

注：这不是 D 老师讲的。

根据定义就可以知道。只需要枚举 $[1,n-1]$ 中所有数，如果这个数与 $n$ 互质，就 cnt++ 。时间复杂度： $O(n \log n)$ （因为 $\gcd$ 的时间复杂是 $\log$ ）。代码：

int ephi_one(int n)
{
	int cnt = 0;
	for (int i = 1; i < n; i++)
	{
		if (__gcd(i, n) == 1)cnt++;
	}
	return cnt;
}

方法二：分解法

根据性质四的公式，可以得到方法：分解 $n$ 的质因数，算进公式里。时间复杂度： $O(\log n)$ ，直接比暴力法少了个 $n$ 。代码：

int ephi_two(int n)
{
	int ret = n;
	for (int i = 2; i * i <= n; ++i)
	{
		if (n % i == 0)
		{
			ret = ret / i * (i - 1);
			while (n % i == 0)n /= i;
		}
	}
	if (n > 1)ret = ret / n * (n - 1);
	return ret;
}

---

1. 前言 ↩︎

2. 数论函数 ↩︎

3. 欧拉函数 ↩︎