前言^[1]

吐槽一下

看到有些人做笔记都是借鉴（你懂的）Wiki 和网上其他资料的。 D 老师上课讲的不好吗？

目录：

• 前言
• 加法原理
• 乘法原理
• 排列
• 组合
• 计数方法
• 特殊排列

---

加法原理^[2]

概念： 如果一个问题有 $n$ 中情况，每种情况有 $m_i$ 种方法，则解决这个问题有 $m_1+m_2+...+m_n$ 种方法。

乘法原理^[3]

概念： 如果一个问题能分成 $n$ 步，每步有 $m_i$ 种方法，且解决这个问题必须连续 $n$ 步，则解决这个问题有 $m_1\times m_2\times ...\times m_n$ 种方法。

加法、乘法原理例题

在 $1$ ~ $2018$ 中含有数字 $8$ 的数有多少个？

可以算出 $1$ ~ $10$ 中有多少个数字含有 $8$ ，然后可以根据乘法原理算出 $1$ ~ $79$ 和 $90$ ~ $100$ ，再用加法原理加上 $80$ ~ $89$ 的数字，算出 $1$ ~ $100$ 的数量。以此类推。

最终答案： $544$ 。

也有其他做法（ D 老师上课讲的）：算出个位是 $8$ 的、十位是 $8$ 的和百位是 $8$ 的，加起来。也可以算出答案。

排列^[4]

定义： 从 $n$ 个数据中选出 $m$ 个数据按照一定顺序排列，叫做排列。记做 $P^m_n$ 。

判断两个排列相同，不仅要数据相同，还要保证排列的顺序相同。

公式

$$P^m_n=A^m_n=\frac{n!}{(n-m)!}$$

展开之后就是这样： $\frac{n\times...\times(n-m)\times...\times1}{(n-m)\times...\times1}$ ，可以发现分子和分母都有 $(n-m)\times...\times1$ ，因此可以约分。约分后就是这样：

$$P^m_n=n\times(n-1)\times...\times(n-m+1)\texttt{（总共 }m\texttt{ 个数）} $$

所以最后的公式就是从 $n$ 开始倒数 $m$ 个数的乘积。

例如从 $3$ 个数中选出 $2$ 个数的排列情况：

1:1 2
2:1 3
3:2 1
4:2 3
5:3 1
6:3 2

一共有 $6$ 种，即 $\frac{3\times2\times1}{1} = 3\times2=6$ 。

组合^[5]

定义： 从 $n$ 个数据中选出 $m$ 个数据出来组成一个组，叫做组合。

判断两个组合的相同，只需要判断数据是否相同，不需要考虑顺序。

公式

$$C^m_n=(^n_m)=\frac{n!}{m!(n-m)!}$$

方便的方法： $C^m_n=C^{n-m}_n$ 。当 $m>\frac{n}{2}$ 的时候就可以这样。例如从 $5$ 个数中选 $3$ 个数组合：

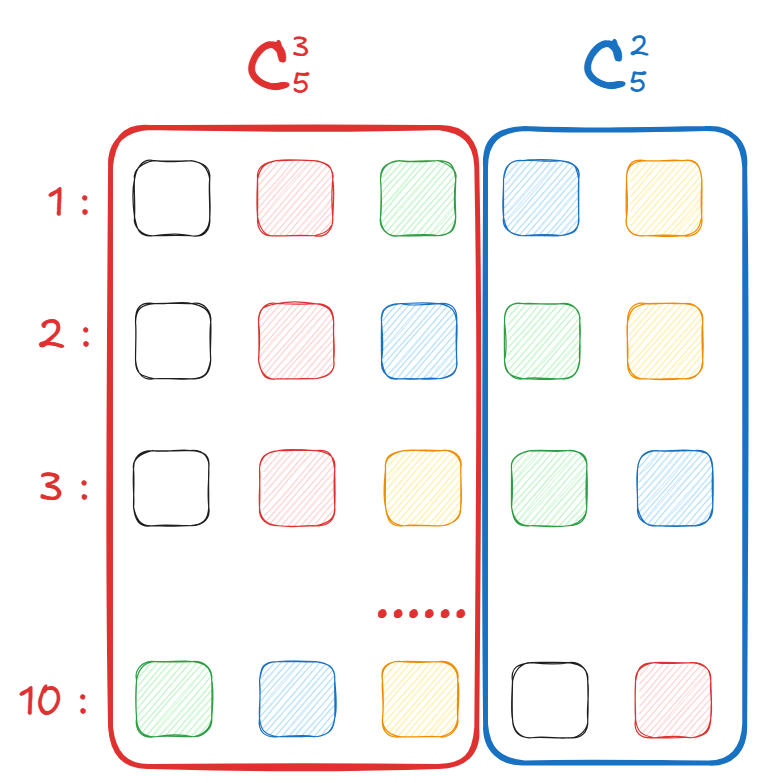
可以发现红色框和蓝色框的数量是一致的，即 $C^m_n=C^{n-m}_n$ 。可以这样想：要在 $n$ 个人中留下 $m$ 个人，可以选择留下 $m$ 个人或踢出 $n-m$ 个人。

因此，如果要算 $C^3_5$ ，可以只算 $C^2_5$ 。

方便记忆的方法： 组合就是在排列的基础上去掉数据一致但顺序不同的，这个数量就是 $m!$ 。

特例

1. $0!=1$ 。这个毫无疑问。

2. $C^0_n=C^n_n=1$ 。这可以根据上面方便的方法推导出来。而 $C^0_n$ 就是 $0!$ 就是 $1$ 。

3. $C^m_n=C^m_{n-1}+C^{m-1}_{n-1}$ 。

   这里用到了类似动态规划的思想。对于第 $n$ 个人，有选和不选两种情况。

   • 如果选：那么就是在剩下 $n-1$ 个人中选 $m-1$ 个名额。即 $C^{m-1}_{n-1}$ 。
   • 如果不选：就是在剩下 $n-1$ 个人中选 $m$ 个名额。即 $C^m_{n-1}$ 。

   根据加法原理，把这些情况加起来就好了。

计数方法^[6]

警告：难度飙升！！！

特殊优先

课件是这样讲的：特殊元素，优先处理；特殊位置，优先考虑。

例题：六个人站成一排，求：

1. 甲不在排头，乙不在排尾的排列数。

   

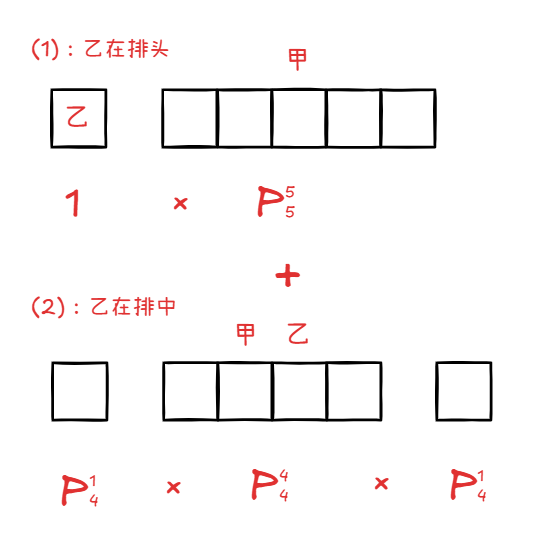
分两种情况：

• 乙在排头：

  那么剩下的人可以随便选择排列。

  数量就是 $P^5_5$ 。

• 乙在排中：

  甲和乙都在排中，那么排头和排尾分别需要一个人。去掉甲和乙的四人种人选。剩下的排中就是任意排列 $P^4_4$ 。

最后的答案就是 $P^5_5+P^1_4+P^4_4+P^1_4=504$ 。

2. 甲不在排头，乙不在排尾，且甲乙不相邻的排列数。

捆绑法

如果要求某些元素需要相邻，可以把这些元素看称一个整体，将这个整体与其他元素排列。根据乘法原理，答案就是整体外排列 $\times$ 整体内排列。

例：有 $6$ 个人排队，要求甲和乙要相邻，求有多少种排列方法？

把甲和乙看称一个整体，排列数就是 $P^5_5=120$ 。甲和乙内部的顺序可以调换，排列数是 $P^2_2=2$ 。总体的排列数就是 $P^5_5\times P^2_2=120\times2=240$ 。

捆绑法求不相邻见排除法。

例 $2$ ：把 $7$ 不同的个球放进 $6$ 个不同的盒子里的方法数。要求每个盒子至少要有 $1$ 个球。

根据抽屉原理，得到有一个盒子会有 $2$ 个球。把这两个球看成一个整体，和其他球放进盒子排列。要注意因为球是没有顺序的，所以是组合。答案： $C^2_7\times P^6_6$ 。

插空法

如果要求某些元素不相邻，可以先将其他元素拍好，再在这些元素的间隙或两端插入要求不相邻的元素，叫做插空法。

例：有 $6$ 个人排队，要求甲和乙不相邻，求有多少种排列方法？

如图：

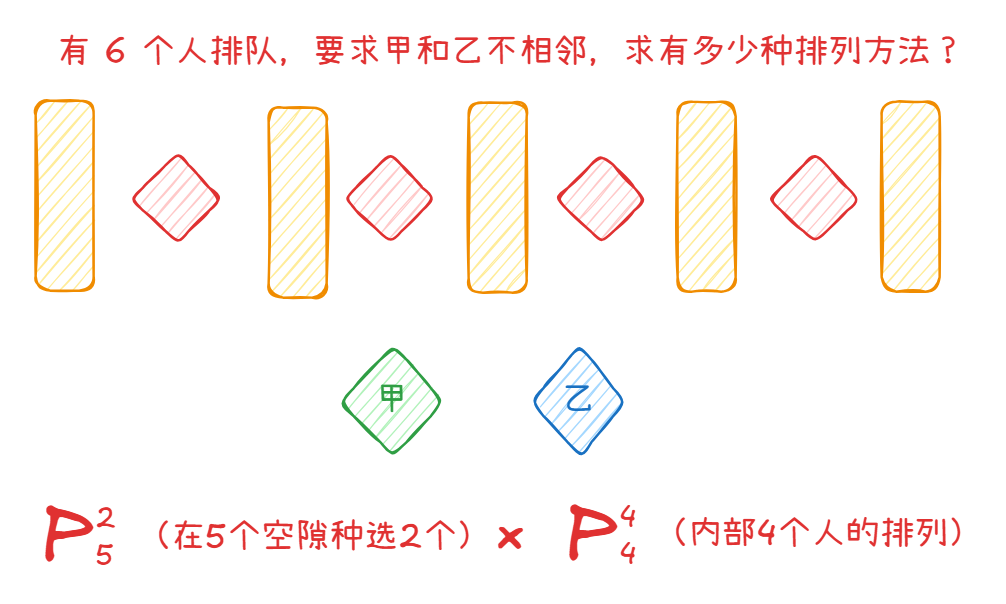
先将其他 $4$ 人排列，有 $P^4_4$ 种情况。再让甲和乙在剩下 $4$ 个人之间和两边的空隙中选出 $2$ 个。最后答案就是 $P^4_4\times P^2_5 = 24\times20=480$ 种。

排除法

先计算全部情况，再去除非法的情况，剩下就是答案。

例：有 $6$ 个人排队，要求甲和乙不相邻，求有多少种排列方法？

这可以用插空法做，但是插空法不是排除法。

可以先计算所有人的全排列，再使用捆绑法计算出甲乙相邻的情况。全排列： $P^6_6=6!=720$ 。甲乙相邻的情况： $P^2_2\times P^5_5=2!\times4!=2\times120=240$ 。全排列减去甲乙相邻的情况： $720-240=480$ 。答案和上面相同。

隔板法

要求一些相同的元素分成若干组的情况数，这可以使用隔板法。

例：有 $7$ 个名额，分给 $4$ 个班级，要求每个班级都至少有 $1$ 个名额，求分配情况数量。

可能看起来有点像捆绑法，但是这里要求元素相同 。

可以这样像：有 $7$ 个名额摆成一列，要用隔板把它分成 $4$ 个班的分配情况。如图：

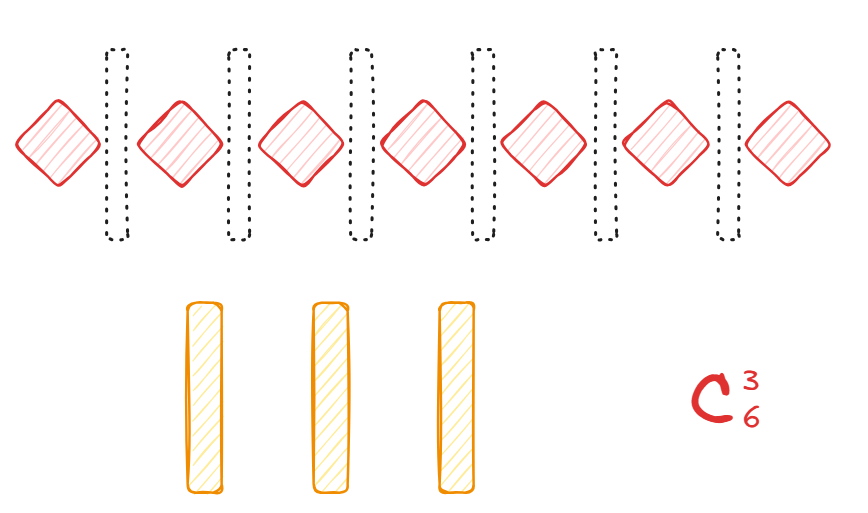
很容易发现结果是 $C^3_6=20$ 种。可以得出公式就是： $C^{m-1}_{n-1}$ 。

隔板法求不定方程解数

不定方程就是类似这样的方程：$x_1+x_2+...+x_m=n$ 。如果有小数或负数的话肯定是行不通的。所以这里只考虑整数。

正整数解数量

可以这样像：把 $n$ 想象成 $n$ 个 $1$ ，要在这 $n$ 个 $1$ 中插入隔板，分成 $m$ 部分。于是又回到这幅图：

带入公式就能求解。

求非负整数解数量

这就有点思维了。设 $y_i=x_i+1$ ，则 $y_1+y_2+...+y_m=n+m$ 。于是问题就转化为求 $y_1+y_2+...+y_m=n+m$ 的正整数解的数量。

可以推导出公式： $C^{m-1}_{n+m-1}$ 。根据性质，也可以转化为 $C^{n}_{n+m-1}$ 。

特殊排列^[7]

可重复排列

即元素可重复取 （抢答：DFS 时不打标记） 。

例：有数列 $\{1,2,3,4,5,6,7,8,9\}$ ，从（可重复）中选出 $5$ 个，有多少种情况。

如图：

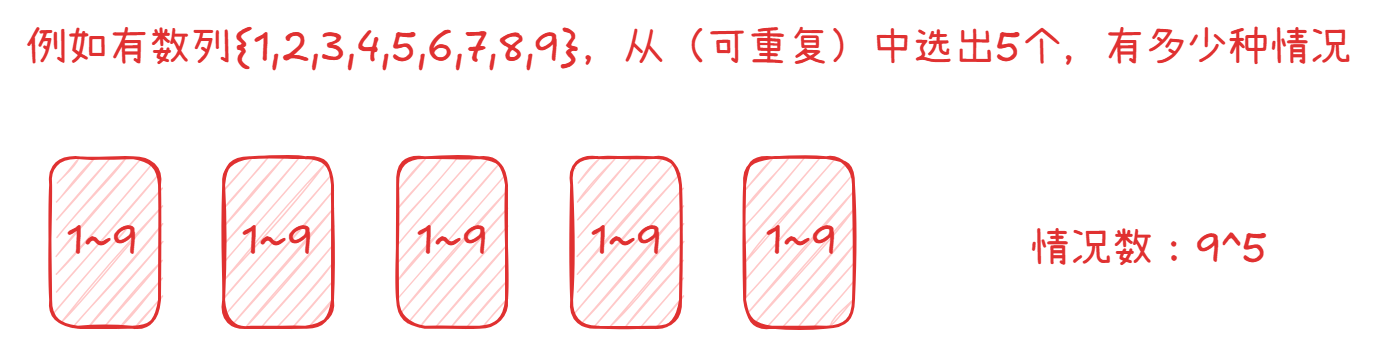
由于可以重复，所以每一个格子都有 $1$ ~ $9$ 的选择，根据乘法原理，答案就是 $9^5$ 。

可以推导出公式： $n^m$ 。

可重复组合

组合数为： $C^{r}_{n-r+1}$ 。

不全相异的全排列

例：有 $5$ 个红球和 $3$ 个白球，求排列方法数。

要注意交换相同颜色的球的排列是不算的。可以使用排除法，先算出所有球的全排列，除以各个球的全排列。

公式： $\frac{n!}{a_1!a_2!...a_k!}$ 。

圆周排列

把 $n$ 个元素排成一个圈，球排列的情况数。

需要注意是一个圆圈，所以旋转的情况不算。

也可以使用排除法。例如选 $3$ 个元素，可以发现 $1-2-3$ 、 $2-3-1$ 和 $3-1-2$ 的排列是一样的，而且数量刚好是 $m$ 。所以可以推导出公式： $\frac{P^m_n}{m}$ 。

---

1. 前言 ↩︎

2. 加法原理 ↩︎

3. 乘法原理 ↩︎

4. 排列 ↩︎

5. 组合 ↩︎

6. 计数方法 ↩︎

7. 特殊排列 ↩︎