- gf24240 的博客
《梦溪笔谈·笔记》2025/8/9~10:容斥、概率&期望、离散、卡特兰数
- @ 2025-8-10 20:30:13
前言[1]
对于昨天没写笔记的事我深感 sorry 可能会写一篇 blog 来说明。还有这篇 blog 收尾有点草率了。最近学的东西都有点抽象,所以能听多少听多少吧。
如有错误请指出。
目录:
集合[2]
在学容斥原理之前(其实要更早)需要先了解集合的概念。
简单来讲(绝对不是严谨的数学定义 ,但我尽量讲的严谨一点 ),集合是一类相同的东西,用集合把他们装起来。例如这是小于 的奇数(奇数本身就为自然数)集合: 。
下面是集合的一些(后面会用到的)运算符号:
补集
设有一个集合 和全集(类似“全部”) 。则 的补集为全集 中不是 的元素。记作 或 、 等。如图:
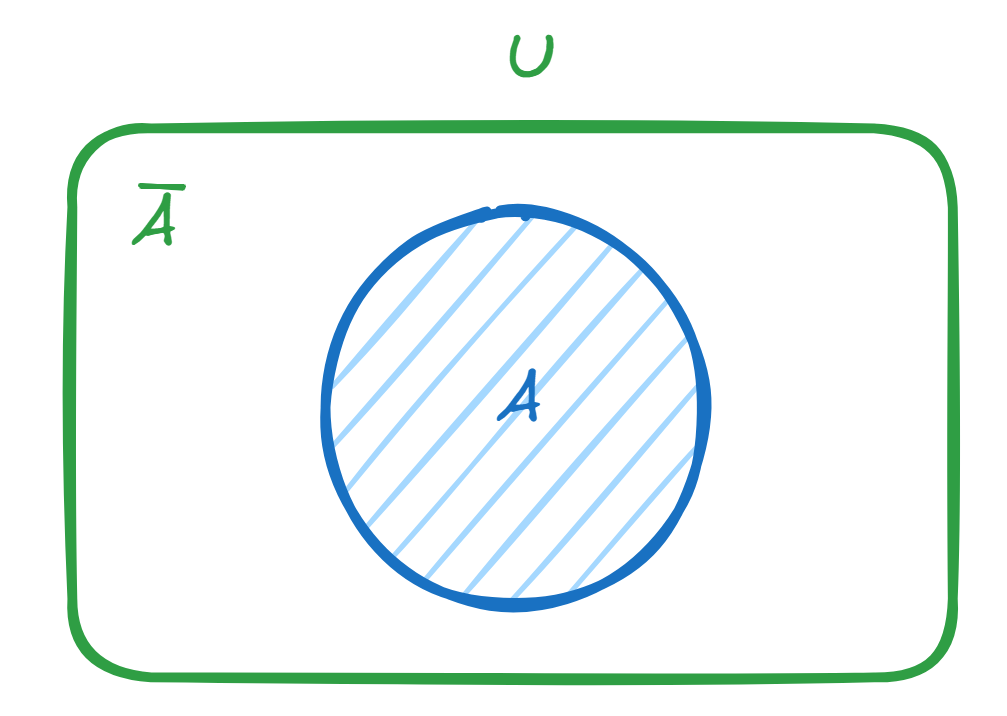
例如 , ,则 。
交集
集合 和 的交集,记作 ,表示集合 和 的集合的共有的部分。如图:
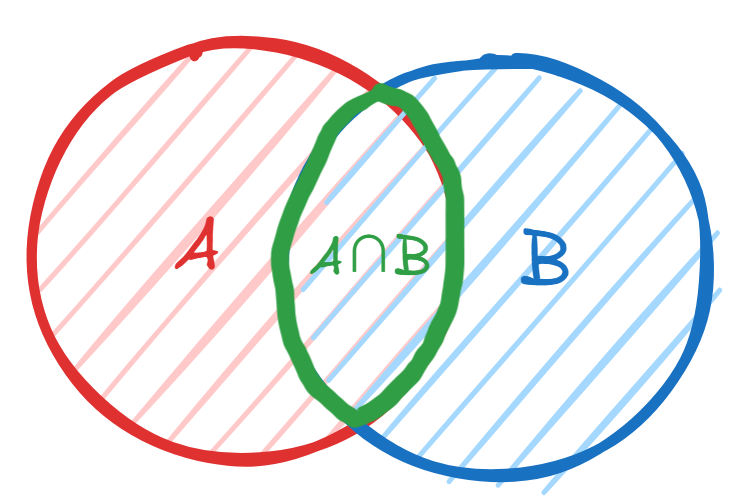
例如:设集合 为 以下能被 整除的正整数(通俗一点就是:是 的倍数的正整数) 的集合,即 。集合 为 以下能被 整除的正整数的集合,即 。很容易想到 。
并集
集合 和 的交集,记作 ,表示集合 和 的集合的全部部分。如图:
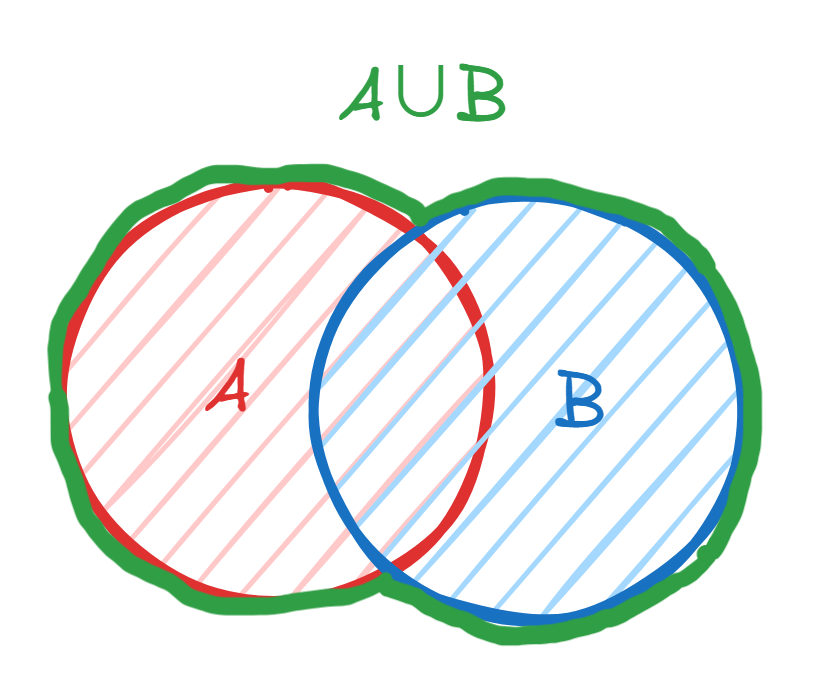
例如:设集合 ,集合 。那么 。
容斥原理[3]
两个集合内的容差关系
举个例子:一个农🏀场有🐔, 只🐔有中分头, 只🐔穿背带裤, 只🐔是既有中分头又穿背带裤。那么问题来了:这个农🏀场一共有几只🐔?
你可能会这样想:直接 不就好了吗?但是我既然问了肯定就不是。还是回到这张图上来(绝对不是为了节省文件):

设集合 为有中分头的🐔,集合 为穿背带裤的🐔。而中间的 为既有中分头又穿背带裤的🐔。
那么我们要求的数量就是 。可以发现直接 是不行的,这样会多加一次中间的部分。所以要减去重复的部分。这样就能推导出公式: 。
这样就能解决🐔问题了: $\texttt{总共数量}=\texttt{中分数量}+\texttt{背带裤数量}-\texttt{坤坤数量}$ 。带入具体数字,得到: 。所以这个农🏀场的🐔数量为 只因。
其实在前缀和问题中也使用到了类似的思想。
三个集合也可以这样推导:
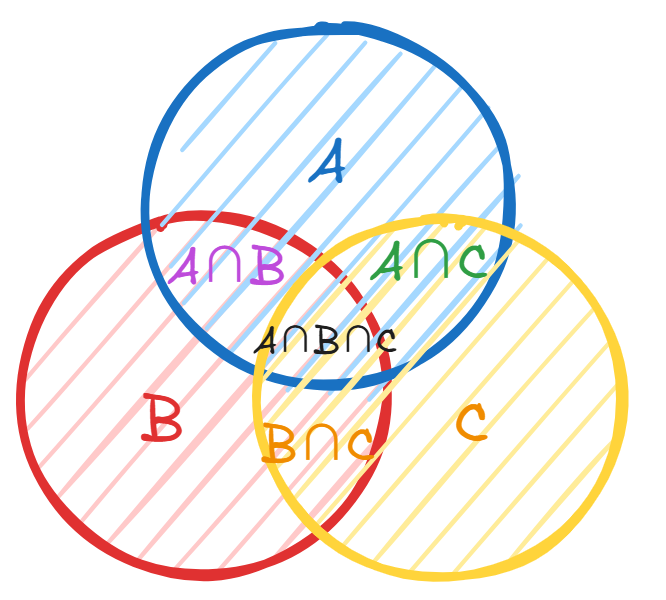
首先加上集合 、 和 。这样会重复,所以要减去它们分别重复的部分: 、 、 。但是这样又双重复了,所以再加上这三个部分的重复,即 。于是就能推导出公式: 。
多个集合
观察上面的公式也许就能发现一点规律了:集合重叠数为奇数时加,反之为减。
设有 个集合,分别是 ~ 。可以推导一下公式:
$$|\bigcup^n_{i=1}A_i|=\sum^{n}_{i=1}|A_i|-\sum^{n}_{i,j:i≠j}|A_i\cup A_j|+\sum^{n}_{i,j,k:i≠j≠k}|A_i\cup A_j\cup A_k|...$$( 应该表示集合 的元素数量)
不要看公式这么复杂,其实就是:$\texttt{所有集合的并集}=\texttt{所有集合}-\texttt{两个集合的并集}+\texttt{三个集合的并集}-......$ 。
错位排列
错位排列,指对于 ~ 的全部排列, 与 都不对应。求全错位排列数。
设 表示 在原来的位置上的排列数。则错位排列数为: 。
根据上面容斥原理的公式,需要先计算 。因为 表示表示 在原来的位置上的排列数,所以任选一个数固定住,剩下的 个数任意排列。因此结果为 。化简得到 。
以此类推, , 有 个数固定,其他 个数任意排列时的排列数为:
$$C^k_n\times (n-k)!=\frac{n!}{k!\times (n-k)!}\times (n-k)!=\frac{n!}{k!}$$再带入容斥原理:
$$1-\frac{n!}{1!}+\frac{n!}{2!}-\frac{n!}{3!}+...+(-1)^n\frac{n!}{n!}$$根据乘法分配律:
$$n!(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+...+(-1)^n\frac{1}{n!})$$这就是错位排列的公式。
例题:装信封问题 。
概率[4]
等可能事件概率
如果一个实验会出现 和结果,事件 的结果出现了其中的 种。则事件 发生的概率为 ,记作 。
几种事件和概率
互斥事件
互斥事件是指几种事件不可能同时发生。
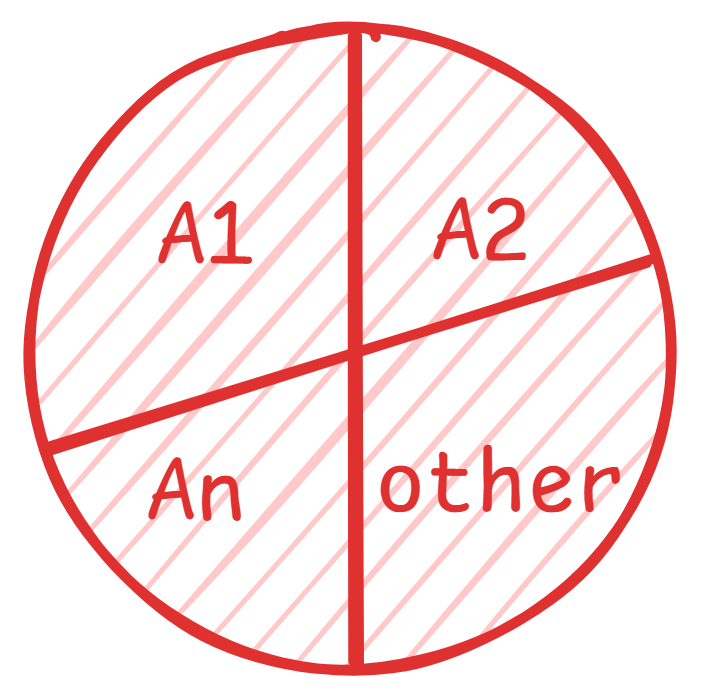
如果事件 互斥,那么这些事件种至少发生一件的概率是: 。
对立事件
对立事件是指:如果事件 和 互斥,且 和 必须发生一件,则称事件 和 对立。
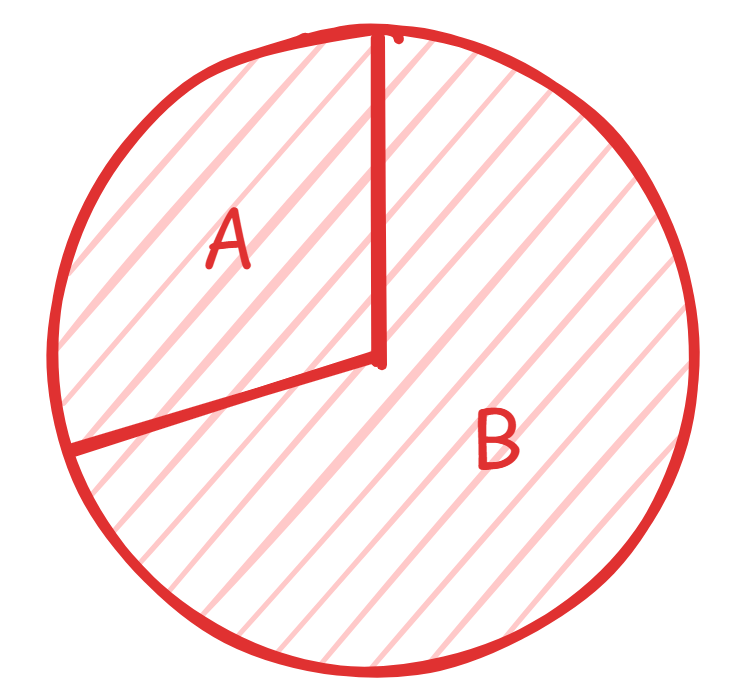
事件 的对立事件记为 。则 (由定义可得) 。
独立事件
如果事件 和 都对对方的概率没有影响,则称事件 和 互相独立。

因为事件 和 都是独立的,所以在 的概率 发生完之后 也有 的概率发生。根据乘法原理, 和 都发生的概率为 。
独立重复实验
独立重复试验,就是多个独立事件。
如果一个事件发生的概率为 ,则独立重复 次实验,该事件发生 次的概率为 。
期望[5]
数学期望,又称均值,或简称期望。是所有实验中概率乘以结果的总和(有点太数学了)。例如:某地有 户家庭,其中没有孩子的家庭有 户,有 个孩子的有 户,有 个孩子的有 户,有 个孩子的有 户。
有 个孩子的概率为 ;
有 个孩子的概率为 ;
有 个孩子的概率为 ;
有 个孩子的概率为 。
因此期望为:
$$\texttt{(实验结果} \times \texttt{概率)} \\ 0\times 0.01+1\times0.9+2\times0.06+3\times0.03=1.11$$可以计算出此地平均每户有 个孩子。
离散数学[6]
字面意思。不同于普通的数学。例如:
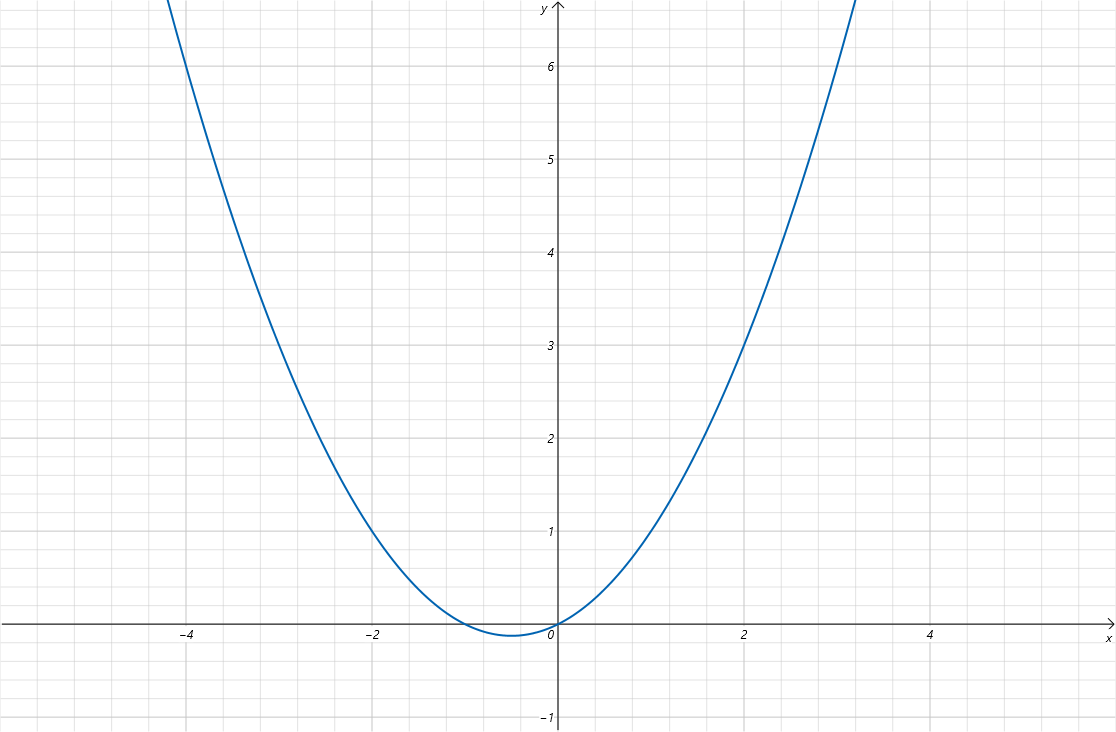
普通数学是连续的,离散数学是离散的。
逻辑运算
这个都熟悉。分别有:
- 与运算: 。都为 true 才为 true;
- 或运算: 。有 true 就为 true;
- 非运算: 。true 为 false , false 为 true ;
- 异或运算: 。不同才为 true 。
运算时要注意优先级。优先级高的先算,优先级相同从左往右运算。
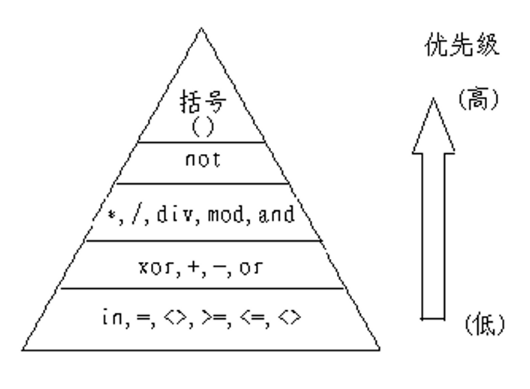
集合运算
如上。
卡特兰数[7]
卡特兰数是一个有点规律的数列,但是又没有具体含义。
例如这些都是卡特兰数:
- 个节点能组成多少种不同的二叉树;
- 个节点依次入栈,有多少种出栈顺序;
- …………(还有很多)。
下面是卡特兰数的计算方法。
递归计算
$$f_n=f_0\times f_{n-1} + f_1\times f_{n-2} + ... + f_{n-1}\times f_{0}$$递推计算
通项式计算
化简后得到:
这是卡特兰数的前几项(从 开始):
简单来说,只要你发现答案的数列是这条,就可以根据卡特兰数的计算方法来计算了。
