前言

之前一直没有实际地弄懂哈夫曼编码。直到暑假初赛集训在发现哈夫曼编码一个很重要的信息。其实之前有过详解（ 数论 、 哈夫曼树&二叉搜索树 ），这里主要纠正一个错误。

---

编码

在日常生活中，我们经常要对信息进行编码（由于电脑使用二进制存储）。

例如我们要对一段文本进行编码，这段文本中：

1. $\texttt{a}$ 出现了 $1$ 次；
2. $\texttt{b}$ 出现了 $1$ 次；
3. $\texttt{c}$ 出现了 $2$ 次；
4. $\texttt{d}$ 出现了 $4$ 次；

下面是一些编码方式：

等长编码

这很容易理解。给每一个出现的字符都给出一段长度相等的编码。例如：

$$\Large \texttt{a:00} \\ \texttt{b:01} \\ \texttt{c:10} \\ \texttt{d:11} $$

如果这样编码，这段文本的长度就为： $1\times2+1\times2+2\times2+4\times2=16$ 。

但是这样也有问题：如果文本出现的个数多，那么编码的长度也会越长。

解码

要解码，只需要按照长度截取，跟表上对照就好了。

不等长编码

这也很好理解。就是长度不一样的编码。随便编。例如：

$$\Large \texttt{a:01} \\ \texttt{b:10} \\ \texttt{c:0} \\ \texttt{d:1} $$

如果这样编码，这段文本的长度就为： $1\times2+1\times2+2\times1+4\times1=10$ 。

解码

这样编码确实短，但是解码就不方便了。按照上面的表，这段：$\texttt{0100}$ 编码你要怎么解？是 $\texttt{acc}$ ？ $\texttt{cbc}$ ？还是 $\texttt{cdcc}$ ？

造成这个问题的原因是：一些编码是另一些编码的前缀。例如在这个编码中， $\texttt{c}$ 是 $\texttt{a}$ 的前缀、 $\texttt{d}$ 是 $\texttt{b}$ 的前缀。

哈夫曼编码

哈夫曼编码的思想是： 出现频率越高，编码越短。可以发现，哈夫曼编码采用贪心思想。

具体步骤是：

1. 先对文本统计出现频率；
2. 每个文本和其对应的频率结合成一个节点；
3. 拿出两个出现频率最小的节点作为左右儿子，用它们的出现频率之和作为一个新的节点，这个新的节点作为它们的父节点；
4. 重复第 $3$ 步，直到没有多余的节点；
5. 组成编码。可以在左边标为 $1$ 或右边标为 $1$。

这棵节点组成树就叫做哈夫曼树 。例如上面的例子：

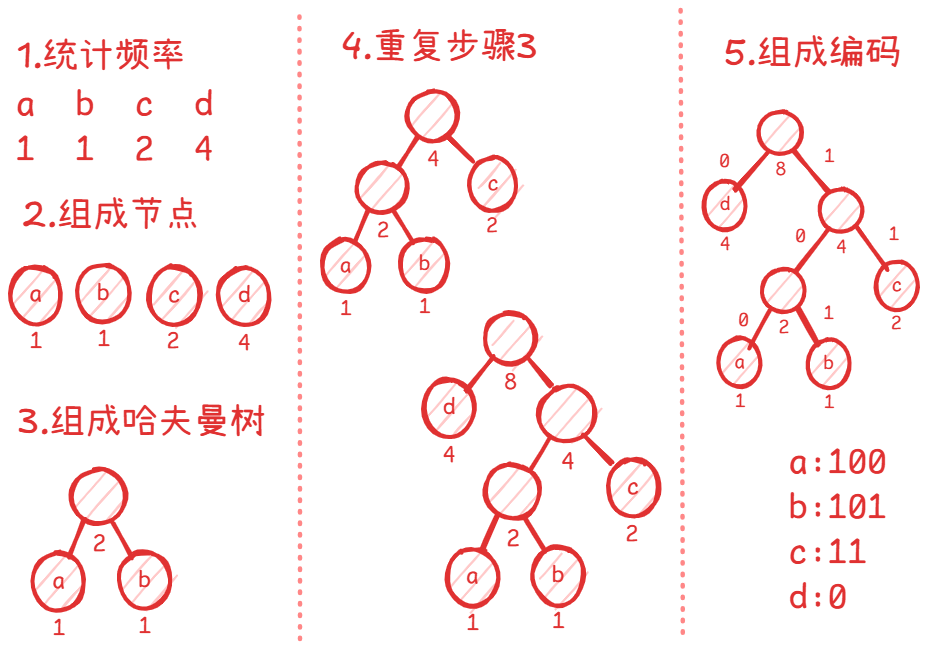
因此得到：

$$\Large \texttt{a:100} \\ \texttt{b:101} \\ \texttt{c:11} \\ \texttt{d:0} $$

这样编码的长度为： $1\times3+1\times3+2\times2+4\times1=14$ 。

哈夫曼编码有几个特点：

1. 是一个合法编码（没有前缀）；
2. 在合法编码中最短。

解码

对应表就好了。

哈夫曼编码注意事项

在组成新节点时不一定只能在原来的树上添加节点（或者说不一定（除了第一次）每次只能拿一个组合节点和一个文本节点）。例如：

1. $\texttt{a}$ 出现了 $1$ 次；
2. $\texttt{b}$ 出现了 $1$ 次；
3. $\texttt{c}$ 出现了 $2$ 次；
4. $\texttt{d}$ 出现了 $2$ 次；

下面是只能拿一个组合节点和一个文本节点结合的哈夫曼树和正确的哈夫曼树对比：

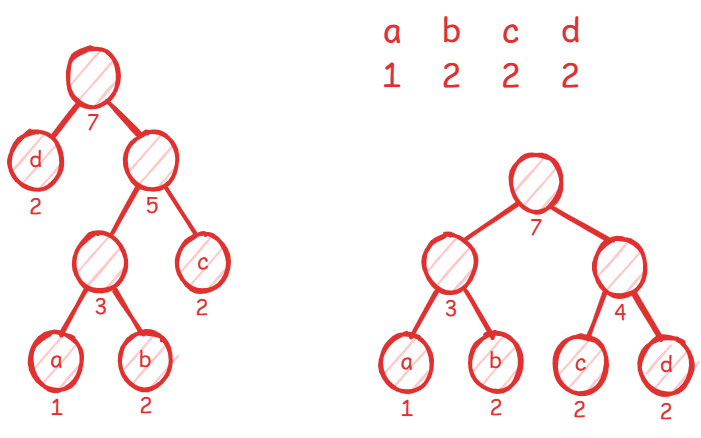
左边的错误示范的编码：

$$\color {red} \Large \texttt{a:100} \\ \texttt{b:101} \\ \texttt{c:11} \\ \texttt{d:0} $$

长度为： $15$ 。

正确的哈夫曼树的编码：

$$\Large \texttt{a:00} \\ \texttt{b:01} \\ \texttt{c:10} \\ \texttt{d:11} $$

长度为： $14$ 。

看到这个（正确的）编码，你是不是想到了等长编码？所以这是得出的结论：在频率相近时，哈夫曼编码会退化为等长编码。