P5286 [HNOI2019] Fish

Problem Description

Note: Source from Luogu.

The data for this problem says there are no issues

Problem Description

In a plane coordinate system, given $n$ distinct integer points (i.e., points with both x and y coordinates as integers), we define an ordered sextuple $(A,B,C,D,E,F)$ formed by selecting six distinct points from these $n$ points as a "fish" if and only if:

• $AB = AC$, $BD = CD$, $DE = DF$ (the body must be symmetric),
• $\angle BAD$, $\angle BDA$, $\angle CAD$, and $\angle CDA$ are all acute angles (the head and tail cannot be concave),
• $\angle ADE$ and $\angle ADF$ are greater than $90^\circ$ (i.e., obtuse or straight angles, ensuring the tail does not appear awkwardly raised).

The following image is an example of a legal fish:

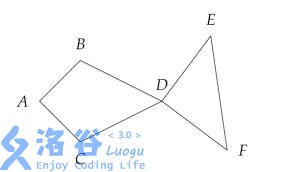
Fish with identical points but different sequences are considered distinct, meaning $(A,B,C,D,E,F)$ and $(A,C,B,D,E,F)$ are treated as two different fish (after all, fish have a back and a belly). Similarly, $(A,B,C,D,E,F)$ and $(A,B,C,D,F,E)$ can also be regarded as two different fish (assuming fish tails can be tied in knots).

How many fish can be formed from the given $n$ points? Specifically, the data ensures that the $n$ points are all distinct.

Input Format

The first line contains a positive integer $n$, representing the number of points in the plane.

The next $n$ lines each contain two integers $x, y$, representing the horizontal and vertical coordinates of the points.

## Output Format

Output one non-negative integer per line, representing the number of fish.

Input and Output Example #1

Input #1

eight
-2 0
-1 0
0 1
0 -1
1 0
2 0
3 1
3 -1

Output #1

sixteen

Instructions/Notes

For 62.5% of the data, it is guaranteed that: $n=10$; For the remaining data, ensure: $n=8$;