前言 ^[1]

这是对素数筛的扩展。本篇 blog 需要的知识点： 筛法 、 欧拉函数 。

目录：

• 前言
• 筛法求最小质因数
• 筛法求欧拉函数

---

筛法求最小质因数^[2]

根据线性筛的性质：

线性筛保证每个数只被最小的质因数筛到。

得出：把线性筛代码中的 vis 数组存储 $1$ 改成存储第一次筛到的因数，就能存储最小质因数。时间复杂度： $O(n)$ （同线性筛）。代码：

void make()
{
	vis[1] = 1;
	for (int i = 2; i <= n; ++i)
	{
		if (!vis[i])
		{
			pre.push_back(i);
			vis[i] = i;
		}
		for (auto j : pre)
		{
			if (i * j > n)break; 
			vis[i * j] = j;
			if (i % j == 0)
			{
				break;
			}
		}
	}
}

---

筛法求欧拉函数^[3]

这是欧拉函数的一些性质：

1. 因为欧拉函数是积性函数，所以 $\varphi(xy)=\varphi(x) \times \varphi(y)$ 。例如 $\varphi(6)=\varphi(2) \times \varphi(3)$ 。
2. 如果 $n$ 为质数，那么 $\varphi(n)=n-1$ 。
3. 若 $n=p^k$ ，其中 $p$ 是质数，那么 $\varphi(n)=p^k-p^{k-1}$ 。

根据这些性质，可以大概推出欧拉筛的 $5$ 中情况：

1. $\varphi(1)=1$ 。

2. 如果 $n$ 为质数， $\varphi(n)=n-1$ 。

3. $n = p \times n'$ ：

   (1). 若 $n'\mod p=0$ ，即 $n'$ 是 $p$ 的倍数。例如 $60=2\times 30$ ，而 $60=2\times 2\times 3\times 5$ ， $30=2\times 3\times 5$ 。可以发现， $30$ 和 $60$ 的质因数是相同的。根据欧拉函数：

$$\begin{aligned} \varphi(n) &= n \times \prod^{s}_{i=1} \frac{P_i-1}{P_i} \\ &\texttt{(带入} n=p\times n' \texttt{)}\\ &= p \times n' \times \prod^{s}_{i=1} \frac{P_i-1}{P_i} \\ \end{aligned} $$

可以发现 $n' \times \prod^{s}_{i=1} \frac{P_i-1}{P_i}$ 就是 $\varphi(n')$ 。所以 $\varphi(n)=p\times \varphi(n')$ 。如果 $n'$ 和 $p$ 调换位置的话，也可以看成 $\varphi(n)=\varphi(p)\times n'$ 。

(2). 若 $n' \mod p ≠ 0$ ，即 $n'$ 和 $p$ 互质。根据欧拉公式的性质，很容易得到 $\varphi(n)=\varphi(p)\times\varphi(n')$ 。

4. 类似情况 $3-2$ ，若 $n=i\times j$ ，且 $i$ 、 $j$ 互质， $\varphi(n)=\varphi(i)\times\varphi(j)$

时间复杂度： $O(n)$ （还是线性筛） 。代码：

void make()
{
	phi[1] = 1; // 情况一：φ(1)=1 
	vis[1] = 1; // 顺便存储最小质因数 
	for (int i = 2; i <= n; ++i)
	{
		if (!vis[i])
		{
			pre.push_back(i);
			vis[i] = i;
			phi[i] = i - 1; // 情况二：若n为质数，φ(n)=n-1 
		}
		for (auto j : pre) // 情况三：n=q*n' 
		{
			if (i * j > n)break;
			vis[i * j] = j;
			if (i % j == 0)
			{ // 情况3-1：n' % q == 0 
				phi[i * j] = phi[i] * j;
				break;
			}
			// 情况3-2&&4：n' % q != 0 
			phi[i * j] = phi[i] * phi[j];
		}
	}
}

实际上情况 $3-2$ 和情况 $4$ 是一样的。

例题-P3998 visible lattice points(可见的格点)

类似洛谷 P2158 仪仗队

参考题解： 原文

---

标签：素数筛 + 欧拉函数 + 前缀和优化
难度：提高+/省选-

这篇题解需要用到的知识点： 素数筛 、 欧拉函数 、 欧拉筛 。

---

如果不看题解可能看不出来。例如下图：

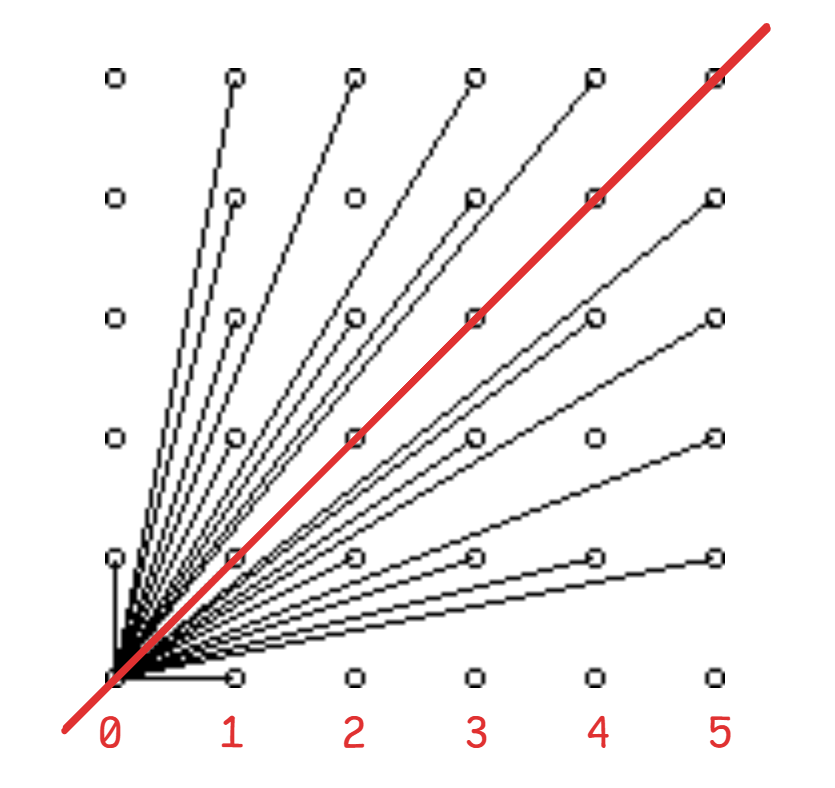
图像可以分为两个一样部分，加上中间的 $(2,2)$ 。而一半中边长为下标时可看见的点数为 $\varphi(i)$ 。最后答案就是 $2 \times \sum^{n-1}_{i=1} \varphi(i) + 1$ 。

由于要求多组，所以先预处理 $1$ ~ $\max(n)$ 的所有欧拉函数，利用前缀和优化。后面访问的时间复杂度就降到 $O(1)$ 。

需要注意的是：当只有 $1\times 1$ 个点时，一个人都不会看到。

总时间复杂度： $O(n)$ 。代码：

#include <vector>
#include <iostream>
using namespace std;

int T, n[1005], maxn, phi[1005], s[1005];
bool vis[1005];
vector <int> pre;

void make()
{
	phi[1] = 1;
	vis[1] = 1;
	for (int i = 2; i <= maxn; ++i)
	{
		if (!vis[i])
		{
			pre.push_back(i);
			vis[i] = i;
			phi[i] = i - 1;
		}
		for (auto j : pre)
		{
			if (i * j > maxn)break; 
			vis[i * j] = j;
			if (i % j == 0)
			{
				phi[i * j] = phi[i] * j;
				break;
			}
			phi[i * j] = phi[i] * phi[j];
		}
	}
	for (int i = 1; i <= maxn; ++i)
	{
		s[i] = s[i - 1] + phi[i];
	}
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	cin >> T;
	for (int i = 1; i <= T; ++i)
	{
		cin >> n[i];
		n[i] = n[i] + 1;
		maxn = (n[i] > maxn ? n[i] : maxn);
	}
	make();
	for (int i = 1; i <= T; ++i)
	{
		cout << i << " " << n[i] - 1 << " " << s[n[i] - 1] * 2 + 1 << "\n";
	}
	return 0;
}

---

以上是参考题解。

---

1. 前言 ↩︎

2. 筛法求最小质因数 ↩︎

3. 筛法求欧拉函数 ↩︎