前言^[1]

暑假要过完了。。。

这段时间（2025/7/16~8/10）的内容：

1. 7/16 ~ 7/21 ：动态规划
2. 7/22 ~ 7/26 ：数据结构
3. 8/1 ~ 8/5 ：数论
4. 8/6 ~ 8/10 ： 数学问题

实际上这篇 blog 更像一个目录。如果有问题请指出。

目录：

1. 前言
2. 动态规划
3. 数据结构
4. 数论
5. 数学问题

---

动态规划^[2]

动态规划（以下简称 DP ）是一种思想。通过把问题分解为 重叠的 子问题，逐个求解，最终得到整体的答案。

DP 的三个特征：

1. 无后效性；
2. 重叠子问题；
3. 最优子结构。

解决 DP 问题的步骤：

1. 分析问题。分析是否符合特征。
2. 定义状态变量。从问题出发。
3. 状态转移方程。合并子问题的解。
4. 初始状态和边界。避免出界。
5. 答案。

线性 DP

参考： 2025/6/26：线性动态规划 、2025/7/16：线性DP&01背包 。

背包 DP

就是一些物品和价值，怎么装最优。

参考： 2025/7/16：线性DP&01背包 、 2025/7/17：背包DP 。

区间 DP

这一块有点阴。

参考： 2025/7/19：区间DP 。

倍增 ST 表

其实这不是 DP ，但是用到了类似 DP 的思路。基本上是套模板。

Log[0] = -1;
for (int i = 1; i <= n; i++)
{
    cin >> a[i];
    f[i][0] = a[i];
    Log[i] = Log[i >> 1] + 1;
}
for (int j = 1; j <= Log[n]; j++)
{
    for (int i = 1; i + (1 << j) - 1 <= n; i++)
    {
        f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
    }
}
for (int i = 1; i <= m; i++)
{
    int l, r;
    cin >> l >> r;
    int k = Log[r - l + 1];
    cout << min(f[l][k], f[r - (1 << k) + 1][k]) << "\n";
}

参考： 2025/7/21：倍增 ST 表 。

数据结构^[3]

应该可以这样称呼，如果图和数也是数据结构的话。

链表

链表可以分为：

1. 动态链表。麻烦又难写的。但是 they （选择题）就是要出动态链表。
2. 静态链表。适合信奥。
3. STL 链表。适合偷懒。

参考： 2025/7/22：链表 。

图

有向图、无向图、稀疏图、稠密图、无权图、甲醛加权图 bala bala bala 都数不过来。

图是由点和边组成的二元组。例如：

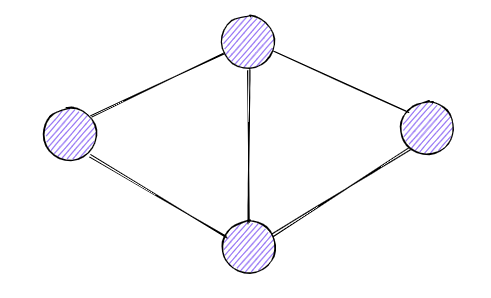
图的存储和遍历可以分为：

1. 邻接矩阵；
2. 邻接链表；
3. 前向星。

参考： 2025/7/23：图的存储和遍历 。

树

树有特殊树（没什么用）、二叉树（很多性质）、二叉树扩展（更多性质了）、哈夫曼树（用于编码）。

参考： 2025/7/23&24：树论 、 2025/7/25：哈夫曼树&二叉搜索树 。

数论^[4]

在数学上的东西。掌握了能掌握。 可能对代码优化有点帮助。

1. 2025/8/1：数论·整除&同余
2. 2025/8/2~3：数论·素数&GCD
3. 2025/8/4：数论·欧拉函数
4. 2025/8/5：数论·筛法扩展

数学问题^[5]

更接近信奥的数学。

1. 2025/8/6~7：数学问题·排列组合
2. 2025/78/8：数学问题·抽屉原理
3. 2025/8/9~10：容斥、概率&期望、离散、卡特兰数

---

1. 前言 ↩︎

2. 动态规划 ↩︎

3. 数据结构 ↩︎

4. 数论 ↩︎

5. 数学问题 ↩︎